Вопрос о делимости числа на произведение его цифр

[gipokrat]

Назовём натуральное число астипоэтическим, если его десятичная запись содержит только цифры 5 и 7, причём в ней имеется хотя бы одна пятёрка и хотя бы одна семёрка.
Может ли астипоэтическое число делиться нацело на произведение всех своих цифр?

[Dmitriy40]

$175$
$1575$
Можно слева дописать любое количество групп по 6 единиц.
$1111111111775$

[maxal]

Так как кратные числа $5^3$ оканчиваются на 000, 125, 250, 375, 500, 625, 750, или 875, то количество пятерок в числе не превосходит 2х, причем последняя цифра - 5.
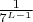
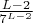
Эмпирически для одной пятерки число длины $L$ будет искомым с "вероятностью" примерно $\frac1{7^{L-1}}$, а для двух пятерок - $\frac{L-2}{7^{L-2}}$. Т.к. сумма этих "вероятностей" по всем $L$ конечна, то нам следует ожидать существования лишь конечного числа искомых чисел. Но так как их нет для малых $L$, то, скорее всего, их не существует вовсе. Подозреваю, что доказать это строго очень сложно.

-- Sun Aug 24, 2025 12:34:50 --

Dmitriy40
Цифра 1 запрещена же.

[lel0lel]

Для одной последней пятёрки, число не будет делиться на $7$.
Если пятёрок две, то последние цифры $75$. Поделим такое число на $25$, тогда получим $77\ldots757\ldots7\cdot 4+3$ или $77\ldots775\cdot 4+3$. Второй вариант не делится на $7$, а первый может. Нужно рассматривать делимость на $7$ числа $4\cdot50\cdot 10^{k}+3$. При $k=6n$ делимость есть, но семёрок становится всё больше) Дальше нужно думать.

[gris]

Можно найти первое число из семёрок и двух пятёрок, которое делится на $25\cdot 7^k$
Например, $5775 \slash (25\cdot 7^1)=33$ и далее
7^1: (4,1)
7^2: (9,6)
7^3: (17,2)
7^4: (56,5)
7^5: (233,50)
7^6: (767,626)
7^7: (1871,1100)
7^8: (3654,273)
7^9: (11278,6043), где выражение (n, m) означает число из n цифр, у которого последняя и m-ная — пятёрки, а остальные семёрки. Увы, признаки делимости на 7 в больших единицы степенях не работают, да и последовательность возрастает, но надежда есть...

[Руст]

Думаю, несложно доказать отсутствие таких.
Единственный вариант $a=77...7577...75=\frac{7*(10^m-1)}{9}-2(10^k+1)$.
Число делится на 25, должен делится на $7^{m-2}$. Число $10^k+1$ делится на 7 тогда и только тогда, когда $k=3+6r$ ($10^3=-1\mod 7$).

Деление на большие степени 7 означает делимость $r$ на большую степень 7.
Нам не обязательно делимость каждого составляющего на большую степень. Однако, проверяя по модулю 49, получим соотношение на $r$ и $m$.
Проверяя по большим степеням $7^k$, получим, что $r,m$ не могут быть меньше $7^{k-1}$, который станет больше $m$ при $k=m-2$.

[maxal]

Руст в сообщении #1699659 писал(а):

Деление на большие степени 7 означает делимость $r$ на большую степень 7.

С чего бы это?

[lel0lel]

Руст в сообщении #1699659 писал(а):

Однако, проверяя по модулю 49, получим соотношение на $r$ и $m$.

Руст
Если положить $r=0$, то есть рассматриваем числа вида $7\ldots7557$, то указанное вами условие сводится к доказательству, что сравнение $10^m-2575\equiv 0\pmod{7^{m-3}}$ не выполняется ни при каких $m>4$. Проверки по малым степеням 7 всегда дают решения, просто эти решения всё возрастают с ростом показателей степеней. Но непонятно, как же строго доказать отсутствие решений. И не видно как получить соотношение на $r$ и $m$.

[Руст]

Если положить $r=0$, то есть рассматриваем числа вида $7\ldots7557$, то указанное вами условие сводится к доказательству, что сравнение $10^m+2575\equiv 0\pmod{7^{m-3}}$ не выполняется ни при каких $m>4$. Проверки по малым степеням 7 всегда дают решения, просто эти решения всё возрастают с ростом показателей степеней. Но непонятно, как же строго доказать отсутствие решений. И не видно как получить соотношение на $r$ и $m$.
При фиксированном $r$ делением на 7 и умножением на 9 получим равенство $10^{m-2}=\frac{a}{4}\mod 7^{m-3}$ (я поделил еще на 25*4).
Период по модулю $7^l$ равен $6*7^{l-1}$. Cоответственно, соотношение
$10^{m-2}=\frac{1+18(1000^{1+2r}+1)}{100}\mod 7^{l}$ не удастся найти при $m>3+6r, l=m-3$.
По видимому, максимальная степень $l$ не превосходит более чем на константу $l$ для случая $m=6*7^{l-1}, k=3*7^{l-1}$.