Электродинамика Джексона после общего курса физики?

[gfgfgf]

Здравствуйте, можно ли изучать электродинамику по книге Джексона после прохождения общего курса физики или это будет слишком сложно и помешает развить интуицию и понимание предмета и лучше для начала пройти какой-то более вводный учебник по электромагнетизму?

[Cos(x-pi/2)]

Так ведь просто попробуйте читать первую главу (и задачи к ней решать), и сразу увидите - годится Вам эта книга или она пока ещё слишком сложная.

[EUgeneUS]

gfgfgf в сообщении #1699360 писал(а):

электродинамику по книге Джексона после прохождения общего курса физики

ИМХО, совершенно неважно, какие курсы физики Вы прошли перед этим.
Важно, какие курсы математики Вы прошли.

-- 23.08.2025, 07:51 --

gfgfgf в сообщении #1699360 писал(а):

помешает развить интуицию

Интуиция - это неосознанный опыт.
В данном случае нарабатывается решением задач.
Какие задачи решаете - такая интуиция и нарабатывается.

[Alex Krylov]

Ну вот возьмем в этой книжке главу 11 "Специальная теория относительности". Может ли после ее прочтения отложиться в голове четкая методология решения задач электродинамики с подвижными объектами/частями (вращательные/линейные электрические моторы, движущиеся/вращающиеся рамки/катушки с током, рассеяние эл.маг. волн на вращающихся телах итд). Однозначно, нет.

А вот тут вышеуказанные вопросы очень хорошо и крайне доступно изложены, есть куча содержательных примеров:
Jean G. Van Bladel - Electromagnetic Fields, Second Edition (глава 17)
Jean G. Van Bladel - Relativity and Engineering

А 1-я книга (из приведенных выше) в общем-то покрывает почти все разделы электромагнетизма.

Еще до кучи:
Griffiths D.J. - Introduction to Electrodynamics. 5-th Edition
Griffiths D.J. - Introduction to Electrodynamics. Solution Manual

William H. Hayt, John A. Buck - Engineering Electromagnetics, 6th Edition + Solutions Manual

Balanis C.A. - Advanced Engineering Electromagnetics

[Утундрий]

Пролистал сабдж. Тяжеловесно и несовременно.

[Alex Krylov]

На самом деле тут каким-то одним учебником трудно обойтись,... или даже тем набором, который я выше привел.

Вот возьмем для примера книжку "Harrington R.F. Field Computation by Moment Methods". Это известная книга, которая в свое время оказала серьезное влияние на развитие всего указанного в названии книги направления, можно сказать, заложила основы. Хорошая, вдохновляющая и окрыляющая книга.

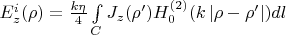
На стр. 41-42 начинает рассматриваться задача рассеяния плоских электромагнитных волн на идеально проводящем (PEC) цилиндре и решение этой задачи с помощью метода моментов. См. интегральное уравнения 3.7, стр. 42: $E_z^i(\rho) = \frac{k \eta}{4} \int\limits_{C}^{}J_z(\rho^\prime)H_0^{(2)}(k\left\lvert \rho-\rho^\prime \right\rvert) dl$. Если бы Харингтон прямо там на стр. 42 (а это только четвертая часть книги!) указал, что с интегральным уравнением 3.7 (это так называемое Интегральное Уравнение Электрического Поля или Electric Field Integral Equation - EFIE) не все так гладко [1-2], то "окрыляющее и вдохновляющее" действие книги могло бы серьезно омрачиться. А суть проблемы состоит в том, что если частота падающей плоской волны сопадает с резонансными частотами сооотв. внутренней полости (с идеально проводящими стенками), то у интегрального оператора, находящегося в правой части уравнения 3.7 появляется нулевое собственное значение [1-2]. В [3] за авторством Poggio A. J. и Miller E.K. (видные авторы, имена которых присутствуют в названии так называемого "метода PMCHWT", P - Poggio, M -Miller, H - Harrington) есть прекрасная (и очень педагогичная) глава 4 - Integral Equation Solutions of Three-dimensional Scattering Problems. И вот там на стр. 223 говорится:

Цитата:

It results from the numerical imprecision of the calculated currents associated with the interior resonance, which while actually non-radiating, because of their numerical inaccuracy do contribute to the far field to such an extent that the overall cross section results are in error. A discussion of integral equation solutions and the difficulties at eigenfrequencies is found in Copley (1968) for the acoustics regime and in Baker and Copson (1953) and Müller (1969) for the electromagnetics regime.

Т.е. авторы (во всем остальном прекрасно написанной главы) полагают (хотя, ЕМНИП, эта проблема была обозначена чуть ли не в самой первой статье, посвященной уравнению типа EFIE; но тут надо уточнить, была ли эта проблема атрибутированна с возникающим нулевым собственным значением или нет), что проблема с уравнениями типа EFIE/MFIE залючается всего лишь "в вычислительных погрешностях" (numerical imprecision, numerical inaccuracy).

Естественно, решению означенной проблемы и получению интегральных уравнений, свободных от указанного дефекта (напр. CFIE - Common Field Integral Eqation, CSIE - Common Source Integral Eqation), посвящено огромное количество статей, и вопрос еще не закрыт.

Да... Как видно из приведенного выше примера с идеально проводящим цилиндром, проблема высвечивается уже для интегральных уравнений, вытекающих (через 3-ю формулу Грина) из скалярного уравнения Гельмгольца в двух измерениях. Т.е. не нужно рассматривать общий векторный случай EFIE/MFIE и иже с ними, это может лишь затуманить суть проблемы. Достаточно рассмотреть скалярное уравнения Гельмгольца и интегральные уравнения, которые из него могут проистекать. Именно этому и посвящена прекрасная обзорная статья [4]. В [4] рассматриваются варианты интегральных уравнений, могущих проистекать их скалярного ур-я Гельмгольца (через 3-ю формулу Грина), и варианты преодоления данной проблемы.

P.S. Так что одной книгой точно не обойтись!!! Ворох все новых и новых проблем и нюансов будет возникать по мере ознакомления с вопросом.
/////////
1. Pierre Steyn, David B. Davidson, A Technique for avoiding the EFIE "Interior Resonance" Problem Applied to an MM Solution of Electromagnetic Radiation from Bodies of Revolution
2. Andrew F. Peterson, The “Interior Resonance” Problem Associated with Surface Integral Equations of Electromagnetics: Numerical Consequences and a Survey of Remedies
3. Computer Techniques for Electromagnetics, Edited by Mittra R.
4. S.I. Zaman, A Comprehensive Review of Boundary Integral Formulations of Acoustic Scattering Problems

[realeugene]

Alex Krylov в сообщении #1700535 писал(а):

А суть проблемы состоит в том, что если частота падающей плоской волны сопадает с резонансными частотами сооотв. внутренней полости (с идеально проводящими стенками), то у интегрального оператора, находящегося в правой части уравнения 3.7 появляется нулевое собственное значение

Так а в чём собственно проблема? Про то, что в колебательном контуре без потерь (у внутренней полости с PEC стенками нет ни резистивных потерь, ни потерь на излучение) можно легко в математической модели получить бесконечную добротность, но потери обязательно на практике там всё-таки есть, и никакой бесконечной добротности на практике не бывает - это вполне очевидно.

[Alex Krylov]

=> realeugene
Тут решается внешняя задача! Мы находимся снаружи бесконечного PEC-цилиндра или PEC-шара. Можем даже сказать, что PEC-цилиндр и PEC-шар являются цельнометаллическими, т.е. там нет никаких полостей, т.е. это не резонаторы (на самом деле это не имеет значения). Далее на этот самый PEC-цилиндр (снаружи) падает плоская эл.маг. волна. Мы хотим получить результирующее поле.

И вот если мы эту задачу (с учетом PEC-граничных условий и условий излучения Зоммерфельда на бесконечности) решаем через уравнения Максвелла, проистекающее из них векторное волновое уравнение или скалярное уравнение Гельмгольца, то все нормально - мы получаем (для всех частот) правильное решение.

А вот если мы переформулируем (еще раз подчеркиваю, внешнюю) эту задачу через интегральные уравнения и ищем распределение поверхностного тока на PEC-объекте через решение интегральных уравнений, то тут получается, что на определенных частотах (падающей плоской эл.маг. волны) интегральные уравнения "разваливаются".

И эти самые частоты, на которых "разваливаются" внешние задачи, решаемые через интегральные уравнения - это не что иное, как собственные частоты соответствующих PEC-полостей (т.е. когда мы решаем задачу на собственные значения внутри соотв. полых PEC-металлических объектов).

[realeugene]

Alex Krylov в сообщении #1700553 писал(а):

И эти самые частоты, на которых "разваливаются" внешние задачи, решаемые через интегральные уравнения - это не что иное, как собственные частоты соответствующих PEC-полостей (т.е. когда мы решаем задачу на собственные значения внутри соотв. полых PEC-металлических объектов).

Ага, интересно, спасибо.

[Alex-Yu]

Alex Krylov в сообщении #1700553 писал(а):

А вот если мы переформулируем (еще раз подчеркиваю, внешнюю) эту задачу через интегральные уравнения и ищем распределение поверхностного тока на PEC-объекте через решение интегральных уравнений, то тут получается, что на определенных частотах (падающей плоской эл.маг. волны) интегральные уравнения "разваливаются".

Не разваливаются. Если не включать внутреннюю поверхность в область интегрирования. Ну если сдуру включить... Так сдуру можно... ...много чего натворить

[Alex Krylov]

=> Alex-Yu

Такое впечатление возникает, что вы не совсем внимательно прочитали всё, что было написано выше... и делаете поспешные суждения.