Решить во взаимно простых целых числах

[nnosipov]

уравнение $(x-y-z)(x+y-z)(x-y+z)=8xyz$.

Комментарий. Задача не моя, но ее автор характеризует ее как open problem. На мой взгляд, ничего сложного (либо я в упор чего-то не вижу).

[wrest]

Очень квадратно.

[nnosipov]

Согласен. И никак иначе. Вот доказать последнее и составляет содержание задачи.

[gris]

А вот числа могут быть отрицательными?
Ну типа $(-3,1,2)$ считается за решение?

[nnosipov]

Давайте исключим (как неинтересные) те $(x,y,z)$, для которых $x+y+z=0$.

[Edward_Tur]

$$(x+y+z)(x-(\sqrt{y}-\sqrt{z})^2)(x-(\sqrt{y}+\sqrt{z})^2)=0$$

[Shadow]

Ну и чтобы поставить точку:

$x=-y-z,\quad \gcd(y,z)=1$

а также

$x= \pm 4q^2$
$y=\pm (p+q)^2$
$z=\pm (p-q)^2$

$\gcd(p,q)=1,\;\; q \ge 1$

$p,q$ разной четности, либо деление на $4$, если $p,q$ - нечетные.

[wrest]

Shadow
$x=1, y=1, z=4$ не вписывается ни в $x=-y-z$ ни в $x=\pm 4q^2$

[Shadow]

wrest,

Shadow в сообщении #1699310 писал(а):

либо деление на $4$, если $p,q$ - нечетные.

$p=-3,q=1$

-- 22.08.2025, 08:23 --

Мне надо было написать $q \ge 0$, чтобы включить и $0,1,1$ но это мелочи. Можно решать в натуральных, чтобы не возится...

[wrest]

Shadow
Загадка какая-то "либо деление на 4" -- что делить на 4?

[Shadow]

wrest в сообщении #1699315 писал(а):

Shadow
Загадка какая-то "либо деление на 4" -- что делить на 4?

Господи...
$x= \pm 4q^2$
$y=\pm (p+q)^2$
$z=\pm (p-q)^2$

$\gcd(p,q)=1$ и $p,q$ разной четности

а также

$x= \pm \dfrac{4q^2}{4}$
$y=\pm \dfrac{(p+q)^2}{4}$
$z=\pm \dfrac{(p-q)^2}{4}$

при нечетных $p,q$

[nnosipov]

Кажется, до меня дошло: если вчитаться в контекст, то в предложении "It is an open problem whether or not there are any other infinite sets of relatively prime solutions." фразу "an open problem" можно понять как "еще одна задача". См. Crux Mathematicorum, V. 21, No. 4, p. 119.

[Shadow]

Цитата:

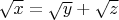
is satisfied by $\sqrt x=\sqrt y+\sqrt z$ Consequently, we also have the infinite set of
solutions
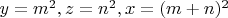
$y = m^2, z = n^2, x = (m+n)^2$ where $(m,n)=1$
It is an open problem whether or not there are any other infinite sets of
relatively prime solutions.

nnosipov в сообщении #1699325 писал(а):

фразу "an open problem" можно понять как "еще одна задача"

Вряд ли, в задаче спрашивается есть ли бесконечно много решений и автор нашел какое-то множество решений (и решал он именно в натуральных числах) и о полноте не задумывался:
Он пишет что-то типа:
Обратите внимание, что если

$x-y-z=2\sqrt{yz},x-y+z=2\sqrt{xz},x+y-z=2\sqrt{xy}$

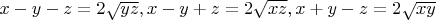
все будет прекрасно и будут вам решениия.

-- 22.08.2025, 10:26 --

Да, его параметризация проще моей