Алгебраическая кривая, построенная по метрическому тензору

[AlexeyE]

Добрый день!

Имеет ли какой-то теоретический смысл следующая кривая на комплексной плоскости переменной z?

Кривая задается матричным произведением вектора-строки на матрицу и на вектор-столбец:
$(1, \bar z, \bar z^2, \bar z^3) G (1, z, z^2, z^3)^T =0$.

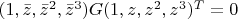
Здесь G - метрический тензор с сигнатурой (1,3), черта над z - комплексное сопряжение.

[Утундрий]

Если $G=\operatorname{diag}(1,-1,-1,-1)$, то, вроде бы, получается окружность.

[AlexeyE]

Да, окружность весьма специфического радиуса, примерно 0.737. Вопрос: имеет ли эта окружность какое-то известное отношение к пространству с такой метрикой? То есть встречал ли кто-нибудь такую окружность в контексте пространств Минковского?

[Утундрий]

Что ещё известно о матрице $G$?

[AlexeyE]

Вообще, достаточно, чтобы у G было ровно одно положительное собственное число. Это единственное важное условие.

[Alex-Yu]

AlexeyE в сообщении #1698841 писал(а):

Имеет ли какой-то теоретический смысл

Если и имеет, то уж точно не физический. Вы ошиблись разделом.