О топологической размерности образа кривой

[Evgenii2012]

Пусть $D$ - область в ${\Bbb R}^n,$ $n\geqslant 2,$ $f:D\rightarrow {\Bbb R}^n$ -- открытое дискретное отображение, $\gamma:[a, b]\rightarrow D$ - кривая без точек самопересечения в $D.$ Верно ли, что топологическая размерность множества $|f(\gamma)|=\{x\in {\Bbb R}^n: \exists\,t\in [a, b]: f(\gamma(t))=x\}$ равна (либо не больше) 1 ? 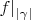(Как представляется, вопрос, по сути, сводится к вопросу, будет ли отображение $f|_{|\gamma|}$ открытым отображением в топологии носителя $|\gamma|$ кривой $\gamma$, индуцированной топологией евклидова пространства; см. книгу Куратовский К., Топология, т.2, п.VI, гл. 4, с. 124).

[dgwuqtj]

Что такое дискретное отображение?