Доброго времени суток!
Пытаюсь решить такую задачу.
Меры

и
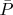
заданы на сигма-алгебре

, причем известно, что
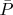
абсолютно непрерывна относительно меры

на алгебре

, т.е. если

, то и
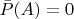
, где
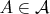
.
Вопрос: является ли
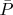
абсолютно непрерывной относительно

на сигма-алгебре

?
Мое решение, где я доказываю, что ответ да.
Решение.Напомним представление, справедливое для каждой вероятностной меры на

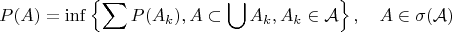
где объединение берется по конечному или счетному набору множеств.
Воспользуемся эквивалентным определением абсолютной непрерывности. Мера
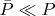
тогда и только тогда, когда для каждого фиксированного

существует

такое что если
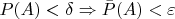
.
Зафиксируем

. Тогда найдется такое

, что для каждого

из

с
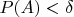
справедливо
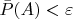
.
Пусть

. Тогда найдется такой не более чем счетный набор множеств
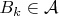
, что
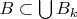
и
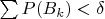
. Поскольку для каждого конечного

множество
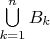
содержится в

и
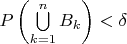
, то
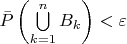
и следовательно
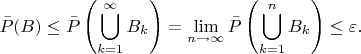
Поскольку это соотношение верно для каждого

, то
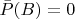
.
В этом решение я использовал эквивалентное определение абсолютной непрерывности, но оно верно, если меры заданы на сигма-алгебре (про его справедливость на алгебре неизвестно).
Может быть это утверждение и не верно?