Случайные величины связанные с sup виннеровско процессы

[seraphimt]

Здравствуйте, дайте намёк, пожалуйста, с парой задач по виннеровскому процессу, вожусь уже несколько дней=_=
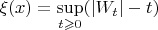
1) Доказать, что случайная величина \xi(x) = \sup \limits_{t \geqslant 0}(|W_t| -t) с вероятностью 1 конечна.
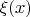
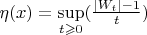
2) Доказать, что случайные величины \xi(x) и \eta(x) = \sup \limits_{t\geqslant0}(\frac{|W_t| - 1}{t}) одинаково распределены.
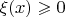
По первому, мне кажется, нужно использовать то, что $\xi(x) \geqslant 0$ т.к. в нуле $(|W_t| -t) = 0$.
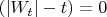
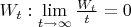
И то, что для винеровского $W_t: \lim\limits_{t\to \infty} \frac{ W_t }{t} =0$(п. н.).
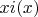
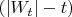
Тогда для $xi(x)$ интересны только "малые" $t$, ведь на "больших" $(|W_t| -t)$ уходит в минус бесконечность.