SO(2) гладким вложенным многообразием и диффеоморфно S1

[AntonioVivaldi]

Рассмотрим пространство матриц $M_2(\mathbb{R})$ как $\mathbb{R}^4$. Докажем, что множество $SO(2)$ ортогональных матриц $2×2$ с определителем 1 является гладким вложенным многообразием и диффеоморфно $S^1$.



Любая матрица из $SO(2)$ имеет вид:

$$ A_\theta = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}, \quad \theta \in [0,2\pi). $$

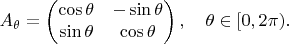
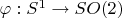
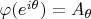
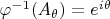
Это задаёт отображение $\varphi: S^1 \to SO(2)$, $\varphi(e^{i\theta}) = A_\theta$. Координатные функции $\cos\theta$, $\sin\theta$ бесконечно дифференцируемы, и обратное отображение $\varphi^{-1}(A_\theta) = e^{i\theta}$ также гладкое, поэтому $\varphi$ является диффеоморфизмом.

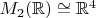
В пространстве $M_2(\mathbb{R}) \cong \mathbb{R}^4$ множество $SO(2)$ задаётся системой уравнений:

$$ \begin{cases} a^2 + b^2 = 1 \\ c^2 + d^2 = 1 \\ ac + bd = 0 \\ ad - bc = 1 \end{cases} $$

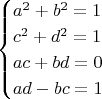
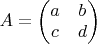
где $A = \begin{pmatrix}a & b \\ c & d\end{pmatrix}$. Матрица Якоби этой системы имеет максимальный ранг, а все уравнения гладкие ($C^\infty$), что показывает, что $SO(2)$ - гладкое вложенное подмногообразие.

А дальше я не знаю, как постоить диффеоморфизм между $SO(2)$ и $S^1$.
Хотелось бы придумать какую-то функцию. Можете навести на мысль?

[Утундрий]

Вы его уже построили.

[AntonioVivaldi]

Утундрий
Прошу прощения и спасибо за внимание