функция ставит конец единичной нормали к тору. Проверить фун

[AntonioVivaldi]

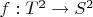
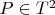
Пусть тор вращения $T^2$ стандартно вложен в $\mathbb{R}^3$. Функция $f : T^2 \to S^2$ ставит в соответствие точке $P \in T^2$ конец единичной нормали к тору в точке $P$, отложенной от начала координат. Записать $f$ в локальных координатах и проверить, что $f$ — гладкая.

Всё ли я сделала верно?

$T^2$ :

$$ \begin{cases} x = (R + r \cos \varphi) \cos \theta \\ y = (R + r \cos \varphi) \sin \theta \\ z = r \sin \varphi \end{cases}, \quad \varphi, \theta \in [0, 2\pi), $$

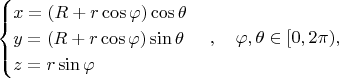
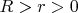
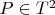
где $R > r > 0$. Отображение Гаусса $f$ сопоставляет точке $P \in T^2$ единичную нормаль $N(P) \in S^2$.



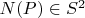
Касательные векторы:

$$ P_\varphi = \frac{\partial P}{\partial \varphi} = (-r \sin \varphi \cos \theta, -r \sin \varphi \sin \theta, r \cos \varphi), $$

$$ P_\theta = \frac{\partial P}{\partial \theta} = (-(R + r \cos \varphi) \sin \theta, (R + r \cos \varphi) \cos \theta, 0). $$

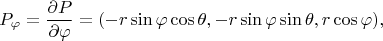
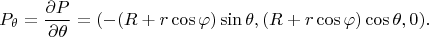
Вектор нормали:

$$ N = P_\varphi \times P_\theta = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ -r \sin \varphi \cos \theta & -r \sin \varphi \sin \theta & r \cos \varphi \\ -(R + r \cos \varphi) \sin \theta & (R + r \cos \varphi) \cos \theta & 0 \end{vmatrix}. $$

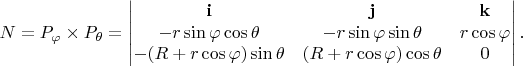
После раскрытия:

$$ N = \left( r (R + r \cos \varphi) \cos \varphi \cos \theta, \, r (R + r \cos \varphi) \cos \varphi \sin \theta, \, r (R + r \cos \varphi) \sin \varphi \right). $$

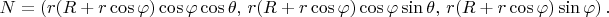
Нормированная нормаль:

$$ N(P) = (\cos \varphi \cos \theta, \cos \varphi \sin \theta, \sin \varphi). $$

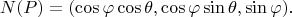
Стереографические координаты на $S^2$:

Для $N(P) = (x, y, z)$:

$$ (u, v) = \left( \frac{x}{1 - z}, \frac{y}{1 - z} \right) = \left( \frac{\cos \varphi \cos \theta}{1 - \sin \varphi}, \frac{\cos \varphi \sin \theta}{1 - \sin \varphi} \right). $$

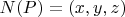
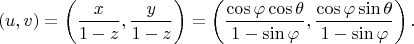
1. Компоненты $N(P)$ гладкие по $\varphi$ и $\theta$ (тригонометрические функции).
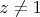
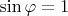
2. Стереографическая проекция гладкая при $z \neq 1$. В точках с $\sin \varphi = 1$ используем вторую проекцию:

$$ (u', v') = \left( \frac{\cos \varphi \cos \theta}{1 + \sin \varphi}, \frac{\cos \varphi \sin \theta}{1 + \sin \varphi} \right). $$

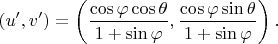
3. Переход между картами гладкий:

$$ (u', v') = \left( \frac{u}{u^2 + v^2}, \frac{v}{u^2 + v^2} \right). $$

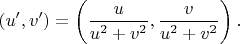
Отображение Гаусса $f$ в локальных координатах:

$$ f(\varphi, \theta) = \left( \frac{\cos \varphi \cos \theta}{1 - \sin \varphi}, \frac{\cos \varphi \sin \theta}{1 - \sin \varphi} \right) $$

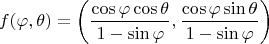
является гладким на $T^2$ благодаря согласованным стереографическим проекциям.