Равномерная непрерывность на ограниченном множестве

[Dedekind]

Задача. Доказать, что если функция $f$ равномерно непрерывна на ограниченном множестве $A$, то множество $f(A)$ также ограниченно.

Мое решение.
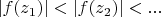
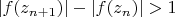
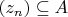
Предположим, $f(A)$ не ограничено. Тогда в нем найдется восходящая неограниченная последовательность $|f(z_1)| < |f(z_2)| < ... $ такая, что $|f(z_{n+1})| - |f(z_n)| > 1$ для всех $n$. Поскольку $A$ ограничено, то соответствующая ей последовательность $(z_n)\subseteq A$ будет ограничена. По теореме Больцано-Вейерштрасса, существует сходящаяся подпоследовательность $(z_{n_k}) \to L$.
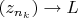
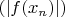
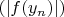
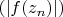
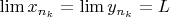
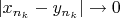
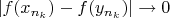
Определим последовательности $(|f(x_n)|)$ и $(|f(y_n)|)$ как состоящие из четных и нечетных членов последовательности $(|f(z_n)|)$ соответственно. Тогда, поскольку $\lim x_{n_k} = \lim y_{n_k} = L$, то $|x_{n_k} - y_{n_k}| \to 0$. Следовательно, по определению равномерной непрерывности, должно быть $|f(x_{n_k}) - f(y_{n_k})| \to 0$. 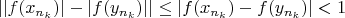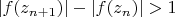Но тогда существует такое $n_k$, что $||f(x_{n_k})| - |f(y_{n_k})|| \le |f(x_{n_k}) - f(y_{n_k})| < 1$, что противоречит предположению $|f(z_{n+1})| - |f(z_n)| > 1$ для всех $n$. Следовательно, $f(A)$ должно быть ограниченным.

Нет ли ошибки в рассуждениях? В решебнике к задаче есть решение, но оно какое-то слишком сложное. Мне кажется, что можно попроще.

[Combat Zone]

Вроде все честно.

[Dedekind]

Combat Zone
Спасибо!