Доказать неравенство

[RikkiTan1]

Доброго времени суток!
Решаю задачу из учебника Ширяева Вероятность 1, глава III $\S 9$ задача 7.
Задача.
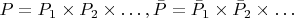
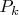
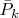
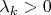
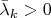
Пусть $ P = P_1 \times P_2 \times \ldots, \bar{P} = \bar{P}_1 \times \bar{P}_2 \times \ldots $, где $ P_k $ и $ \bar{P}_k $ — распределения Пуассона с параметрами $ \lambda_k > 0 $ и $ \bar{\lambda}_k > 0 $ соответственно. Тогда нетрудно показать, что

$$ \bar{P} \ll P \iff P \ll \bar{P} \iff \bar{P} \sim P \iff \sum_{k=1}^{\infty} (\sqrt{\lambda_k} - \sqrt{\bar{\lambda}_k})^2 < \infty, $$

$$ \bar{P} \perp P \iff \sum_{k=1}^{\infty} (\sqrt{\lambda_k} - \sqrt{\bar{\lambda}_k})^2 = \infty. $$

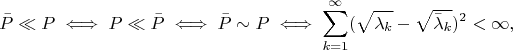
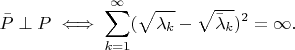Решение. Я нашел интеграл Хеллингера порядка $\alpha$ для $P_k$ и $\bar{P}_k$

$$ H(\alpha,P_k,\bar{P}_k)=\sum\limits_{i=0}^\infty\left(\frac{e^{-\lambda_k}\lambda_k^i}{i!}\right)^\alpha\left(\frac{e^{-\bar{\lambda}_k}\bar{\lambda}_k^i}{i!}\right)^{1-\alpha} =e^{-\lambda_k\alpha}e^{-\bar{\lambda}_k(1-\alpha)}\sum\limits_{i=0}^\infty \frac{(\lambda_k^\alpha \bar{\lambda}_k^{1-\alpha})^i}{i!}$$ $$ =e^{-\lambda_k\alpha-\bar{\lambda}_k(1-\alpha)}e^{{\lambda}_k^\alpha\bar{\lambda}_k^{(1-\alpha)}} =e^{-\lambda_k\alpha-\bar{\lambda}_k(1-\alpha)+{\lambda}_k^\alpha\bar{\lambda}_k^{(1-\alpha)}} $$

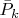
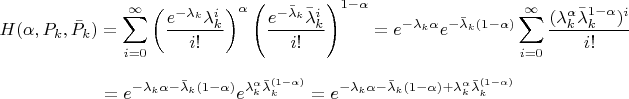
Беря в качестве $\alpha=1/2$, получим, что $H(1/2,P_k,\bar{P}_k)=e^{-\frac{1}{2}\left(\sqrt{\lambda_k} - \sqrt{\bar{\lambda}_k} \right)^2}$.
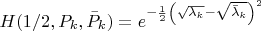
Поэтому

$$ H\left(\frac{1}{2}; P, \bar{P}\right) = \exp\left\{-\frac{1}{2} \sum_{k=1}^\infty \left(\sqrt{\lambda_k} - \sqrt{\bar{\lambda}_k} \right)^2\right\} $$

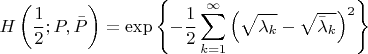
Далее с ортогональностью все становится очевидно.
Чтобы проверить абсолютную непрерывность, нужно показать, что $H\left(\alpha; P, \bar{P}\right) \to 1 $ при $\alpha\to 0$, где

$$ H\left(\alpha; P, \bar{P}\right) = \exp\left\{\sum_{k=1}^\infty -\lambda_k\alpha-\bar{\lambda}_k(1-\alpha)+{\lambda}_k^\alpha\bar{\lambda}_k^{(1-\alpha)}\right\}. $$

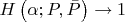
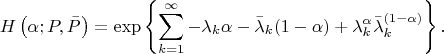
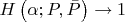
при этом в указании к задаче сказано, что это стремление $H\left(\alpha; P, \bar{P}\right) \to 1 $ есть тогда и только тогда, когда ряд выше сходится при $\alpha=1/2$

$$ \sum_{k=1}^\infty \left(\sqrt{\lambda_k} - \sqrt{\bar{\lambda}_k} \right)^2<\infty.$$

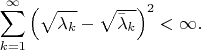
Чтобы доказать утверждение с абсолютной непрерывностью, мне нужно доказать неравенство

$$ \alpha x+(1-\alpha)y+x^\alpha y^{1-\alpha}\leq \frac{x}{2}+\frac{y}{2}-x^{1/2}y^{1/2}, $$

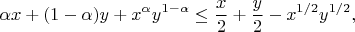
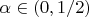
где $x,y$ положительны и $\alpha\in(0,1/2)$. Может быть это какое-нибудь стандартное общеизвестное неравенство, у которого есть название?