Метод "Замороженного ротора"

[sergey zhukov]

При моделировании лопаточных машин используют метод "замороженного ротора". Это некоторое упрощение, при котором ротор относительно статора не вращается. Задача получается стационарной (статическая геометрия) и ее проще решить, чем нестационарную задачу с вращающимся ротором (переменная геометрия).

Я с этим методом только сейчас столкнулся. Правильно я понимаю, что идея тут такая:

Скажем, имеем центробежный одноступенчатый нагнетаталь. Можно сказать, что весь расчет ведется во вращащейся системе координат, причем статор вращается вместе с ротором (они взаимно неподвижны). Вся область потока разбита (руками, условное разбиение) на две части: область внутри колеса и область вне колеса. Внутри колеса расчет в потоке ведется с учетом центробежной и кориолисовой сил. А вне колеса эти силы в потоке просто отключаются. Получается, что вне колеса система отсчета как-бы не вращающаяся, хотя она и неподвижна относительно вращающегося колеса.

Т.е. у нас получается некоторая статичная геометрия проточной части, в одной части которой (колесо) силы инерции вращающейся система отсчета включены, а в другой (вне колеса) - выключены. Правильно?

[Утундрий]

На самом деле идея тут следующая: "За неимением гербовой, пишем на клозетной".

[sergey zhukov]

Немного разобрался в этом приближении. Оно работает так. Вся область решения разбивается (достаточно произвольно) на две подобласти: цилиндрическую область, включающую вращающуюся деталь и внешнюю область, включающую все остальное. Вводятся два поля скорости среды: абсолютная скорость $u$ и относительная скорость $u_r$ (скорость относительно ротора). Связь между ними:

$$u=u_r+\vec{\omega}\times \vec{r}$$

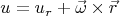
В области вращения решается уравнение Навье-Стокса так, как будто оно решается во вращающейся СО, т.е. с псевдосилами и относительно $u_r$. Во внешней области решается уравнение Навье-Стокса в ИСО, т.е. относительно $u$ и без псевдосил. Оба решения должны сшиваться на границе согласно:

$$u=u_r+\vec{\omega}\times \vec{r}$$

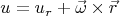
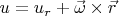
Так получается "вращение среды без вращения геометрии", поэтому решение оказывается стационарным. Общее решение в ИСО получается, если взять поле $u$ вне вращающейся области и поле $u=u_r+\vec{\omega}\times \vec{r}$ внутри области вращения. Решение выглядит немного странно, поскольку линии тока внутри области вращения пересекают поверхности лопаток (создает трудности при визуализации).

На границе двух областей существует разрыв объемных сил (там псевдосилы внезапно обрываются). Решение зависит от того, как именно выбрать область вращения вокруг вращающейся геометрии (захватить больше или меньше пространства вокруг нее).

Существует два предельных случая: колесо с бесконечным числом лопастей и колесо с конечным числом лопастей, вращающееся в бесконечном свободном пространстве, заполненном средой. В первом случае решение в ИСО, очевидно, будет стационарным (всю задачу можно решать в ИСО без разбиения на две области). Во втором случае наоборот, решение во вращающейся СО будет стационарным (всю задачу можно решать во вращающейся СО без разбиения на две области).