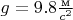Бусинки

[maxmatem]

Надеюсь эта задача окажется поинтереснее


Две одинаковые маленькие бусинки могут двигаться без трения по гладкому горизонтальному стержню. Бусинки связаны легкой нерастяжимой нитью длиной $2L=1,5$ м. К середине нити прикреплена еще одна такая же бусинка. Вначале эту (среднюю) бусинку удерживают так, что нить не натянута, но практически не провисает, затем бусинку отпускают, в результате система начинает двигаться без рывков. Найдите скорости всех бусинок в момент, когда расстояние между крайними бусинками равно $2l=1,2$ м . Массы всех трех бусинок одинаковы. Считая массу бусинки $m=0,1$ кг, определите, чему равна сила натяжения нити в этот момент времени

[lel0lel]

Используя ЗСЭ и уравнение связи скоростей, можно найти скорости. Для бусин на спице получается $v^2=\frac{81g}{340}$; для свисающей $u^2= \frac{36g}{85}$. Модуль мгновенного ускорения бусин на спице $\dot{v}=\frac{252}{289}g$. Умножая его на массу, получим равнодействующую силу, а из неё уже натяжение нити.
Upd: Поправил ускорение, оно было записано неверно (ошибся в арифметике).

[revos]

Задача решена в интернете.

[maxmatem]

revosНу ясно, что большинство задач решено в интернете . Но это не повод ее не решать .
Задача хорошая .

[revos]

"Но это не повод ее не решать ."
А какой повод на сайте предлагать решить решённое?

[maxmatem]

revos
Я задачу предложил , тк по моему вкусу она вполне интересна . Странно , что вместо того чтобы ее решать, Вы начали ее искать в интернете .
Ну в конце концов , Вам задача не интересна , так не решайте ее .

Найти уникальную олимпиадную задачу которая не была бы производной от какой то стандартной конструкции достаточно не просто .

Если вы обладаете такими задачами , то пожалуйста выложите их , и я с удовольствием и другие участники ее порешают если она прийдется по вкусу .

[maxmatem]

lel0lel
Я посчитал ваши скорости и они расходятся с ответом . Я как понял в общую формулу для скоростей Вы уже численно подставили L и l ?

[lel0lel]

maxmatem
Перепроверил, получилось тоже самое. Ниже ход решения для скоростей.
Нулевой уровень находится на уровне спицы. Острый угол между нитями и спицей $\alpha\in [0,\pi/2]$. Модули скоростей бусин на спице и свисающей соответственно $v, u$.
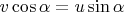
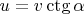
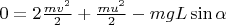
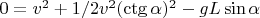
Так как нить нерастяжима и всё время натянута, то проекции скоростей бусин на нить равны, это даёт связь $v\cos \alpha=u \sin \alpha$. Запишем её так $u=v \ctg \alpha$. Полная механическая энергия сохраняется и, в соответствии с выбором нулевого уровня потенциальной, равна нулю: $0=2\frac{mv^2}{2}+\frac{mu^2}{2}-mgL\sin\alpha$ или $0=v^2+1/2v^2(\ctg\alpha)^2-g L\sin\alpha$. Отсюда

$$v^2=\frac{2gL\sin\alpha}{2+(\ctg\alpha)^2}, u^2=v^2(\ctg\alpha)^2.$$

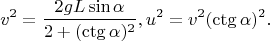
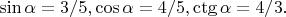
В тот самый момент времени $\sin\alpha=3/5, \cos\alpha=4/5,\ctg\alpha=4/3.$ В итоге получаем:

lel0lel в сообщении #1698271 писал(а):

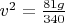
Для бусин на спице получается $v^2=\frac{81g}{340}$; для свисающей $u^2= \frac{36g}{85}$.

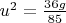
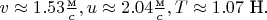
Численные значения скоростей и натяжения нити в тот самый момент такие: $v\approx 1.53 \frac{\text{м}}{c}, u\approx 2.04 \frac{\text{м}}{c}, T\approx1.07 \text{ Н}.$ Это я считал при $g=9.8\frac{\text{м}}{c^2}$

[maxmatem]

lel0lel
Все отлично , я криво посчитал . У вас все верно . Спасибо за внимание к задаче