Первое - исследовать на предмет взаимной простоты базисных решений. Возможны кажется, 2 случая - либо базисные решения попарно взаимно просты, либо имеют вид (3x,3y,z), где x,y,z - попарно взаимно просты.
После этого в обоих случаях можно писать уравнение относительно x,y,z, сразу сократив его на 3.
Далее, упорядочив переменные по возрастанию и учитывая, что сумма двух маленьких чисел должна быть меньше удвоенного большого, сокращая в итоге на общий множитель, останется решить несколько совсем простых уравнений вида:

, либо
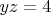
, либо
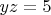
, оставшиеся кажется не имеют решений.
В случае взаимно простых решений первое из этих уравнений даст два ответа. Один из них - (2,3,5) Вы нашли, второй - (1,6,7), оставшиеся два дадут по одному ответу - (1,4,15) и (1,5,9).
Во втором случае последние два уравнения дадут по 2 ответа - (1,12,39), (3,4,21) и (1,15,24),(3,5,12)
Решал устно, возможно упустил еще какие-то решения. Надо все записать и аккуратно перебрать все случаи, их в итоге должно остаться не так много.