EUgeneUSВопрос вот в чём:
Допустим, у меня АЦП 4-битный, MSB отводится на знак. Я решил его отсчёты обработать с фиксированной точкой функцией

. У меня попался отсчёт 0'111 (тут апостроф - отделение знакового бита). Если я говорю, что точка у меня в самом конце и дробной части у меня нет, то получаю ответ: 0'0111000, то есть 56 в десятичной сс. Если я выделяю под дробную часть 2 бита, то ответ уже такой: 0'100.1101, то есть 4.8125. В обоих случаях у меня переполнение, у меня тут два варианта:
1) Изначально уменьшить сигнал так, чтобы результат операции влез в разрядную сетку. Но так я очень сильно потеряю в точности, потому что по сути не буду использовать половину разрядов АЦП.
2) Преобразовать сигнал после вычислений так, чтобы результат влез в разрядную сетку в том же формате, что и до операции (то есть положение точки должно остаться прежним). Причём преобразовывать сигнал в самом конце не вариант, потому что тогда при вычислении функции
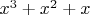
нужно будет увеличивать разрядную сетку не в два, а уже в три раза и так далее. То есть принцип такой: сделали вычисление, вернули его в нужную разрядную сетку, перешли к следующему вычислению. Я выбрал именно этот вариант.
Получается, что в первом случае мы можем даже не выполнять сложение - всё равно оно будет за разрядной сеткой. Возводим 0'111 в квадрат, отсекаем последние 4 разряда и получаем 0'011, погрешность получилась около 14%.
Теперь рассмотрим второй вариант. Возводим в квадрат, двигаем точку и получаем 0'0.11. Точку мы сдвинули влево на 2 бита (поделили на 4), значит и слагаемого должны сделать то же самое. Прибавляем 0'0.01 (сдвинутое влево на два бита 0'1.11) и получаем 0'1.00 и погрешность около 20%.
Теперь вопрос - а какой вариант использовать? И если использовать вариант с точкой, то где её ставить? Есть ли какое-то правило на этот счёт или это определяется экспериментально? Допустим, нужно мне вычислить функцию
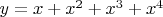
, это получается, что
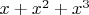
можно и не вычислять даже?