Школьная задача про космический корабль

[RikkiTan1]

Доброго времени суток!
Один мой знакомый по переписке, который сам по профессии врач, но который увлекается физикой, и который сейчас находится под надежной охраной государства, не может найти ошибку в своих рассуждениях в задаче, которую он сам и придумал.
Вот его рассуждения (привожу текст дословно со всеми кавычками).
Представим космический корабль цилиндрической формы, вращающийся для создания искусственной "силы тяжести". т.е. "центробежной силы".
Если взять радиус $r=10$м, то для создания во вращающейся системе отсчета цинтробежного ускорения $a_\text{цб}=10$ $\text{м}/c^2$
угловая скорость должна быть $w=1$ рад/с, линейная скорость "стенки" $v_\text{ст}=10$ м/с, правильно? Теперь представим, что нам удалось прыгнуть "вверх" (к оси вращения) с "начальной скоростью" $v_0=10$ м/с. Из элементарных геометрических построений выходит, что наше тело (в инерциальной системе отсчета) пройдет по хорде $\pi/2$ рад с постоянной скоростью $10\sqrt{2}\sim 14,2$м/с и через секунду "приземлится". За это время "земля"("стенка") сдвинется на 1 рад, т.е. на 10м. А $\pi/2$ рад - это у нас $\sim 15.7$ м. То есть "кориолисова сила" снесет нас аж на $5.7$ м в сторону. Но ведь при этом за секунду полета относительная "горизонтальная" (тангенциальная) скорость составит максимум (в "верхней точке" A ) всего $14.2-10=4.2$ м/с! Так что за 1 сек никак не может получиться $5.7$ м.

Может быть кто-нибудь видит, где в его рассуждения ошибка? Наверное это задача даже школьного уровня, но мною весь этот школьный материал физики и университетский материал теор. меха благополучно подзабыты.

[Theoristos]

Дам рассуждение побочное, но забавное.

Пусть у нас корабль вообще не вращается. Ровнёхонько 0 рад/с.
И космонавт так же прыгает вверх со скоростью 10 м/с.

Тогда за 2 с он пройдёт корабль насквозь и приземлится на противоположной, "верхней" стороне.
Путь от точки старта до приземления окружности равен $10\pi$ метров.
При этом для наблюдателя в этих двух точках "горизонтальная" скорость всё время равна 0. Как так?

Ну, а для наблюдателя на полпути по окружности, "справа", "горизонтальная" скорость на середине пути равна 10 м/с, что при умножении на 2с даёт 20 метров.

Так, что
1. Я бы всё-таки прояснил "интуитивно ясное" понимание этой "горизонтальной скорости".

Ибо, таракану, одновременно пущенному по окружности, чтоб сохранять одинаковую "высоту" с космонавтом нужно в начале бежать с бесконечной скоростью. И только на середине замедлиться до 10 м/с.

А таракан, который постоянно держит космонавта "в зените", вообще обречён оставаться на одном, стартовом месте. И в момент пересечения центра мгновенно телепортироваться в конечную точку.
А если, для снятия вырождения, корабль самую чуточку вращается. Так что космонавт движется чуть в сторону от центра - то такой таракан, держащий космонавта в зените, на середине пути должен бежать по стенке со скоростью гораздо выше 10 м/с, на отношение радиуса к расстоянию космонавта от центра.


2. Пути перемещения таки разные. Космонавт "срезает".

[RikkiTan1]

Большое спасибо за ваш ответ! Мой товарищ будет ему очень рад!

[EUgeneUS]

Вот с этого места начинается какая-то слабо понятная каша:

RikkiTan1 в сообщении #1696727 писал(а):

За это время "земля"("стенка")

Проще взять и зачеркнуть отсюда и до конца текста.

А поступать нужно более аккуратно. Вводя системы координат.
Например так:

1. Ведем систему координат в ИСО: точка отсчета - центр окружности, ось $Oy$ направлена вверх (по рисунку) и проходит через точку старта, ось $Oх$ направлена вправо (по рисунку).
Тогда в этой СК траектория, параметризированная временем:

$$x = 10t; y = 10(-1+t)$$

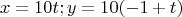Вот тут нарисовано в Вольфраме для наглядности.

2. Далее перейдем в неИСО и построим там систему координат.
i. Пусть также $Oy$ проходит через точку старта, но теперь точка старта вращается вместе с окружностью.
За время $t$ система координат повернётся на угол $\varphi(t) = \omega t$
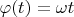
ii. пересчитаем координаты через поворот на угол $\varphi(t) = \omega t$:

$$x_1 = x \cos \varphi + y \sin \varphi = 10 (t \cos (t) + (-1+t) \sin(t))$$

$$y_1 = - x \sin \varphi + y \cos \varphi = 10 (- t \sin (t) + (-1+t) \cos(t))$$

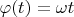
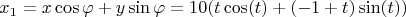
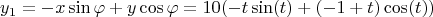Вот тут нарисовано в Вольфраме для наглядности

-- 08.08.2025, 18:00 --

И вот только теперь, если есть желание, можно дифференцировать $x_1, y_1$ по времени один или два раза и что-то с чем-то сравнивать.
А не рассуждать про мифическую "тангенциальную" скорость.

-- 08.08.2025, 18:16 --

Ещё, например, можно повернуть оси системы координат в неИСО, так чтобы траектория была симметричной относительно какой-нибудь оси.
Выглядеть это будет примерно вот так.
И уже в этой СК рассматривать перемещения, скорости и ускорения вдоль осей.

В общем, мораль сей басни такова: перед тем как рассуждать о перемещениях, скоростях и ускорениях вдоль осей системы координат, эту систему координат надо построить.

[RikkiTan1]

Большое спасибо! Отлично, то что нужно!