А область целостности обязана содержать единицу?
Да, в этой книге единица входит в определение области целостности.
Но ИМХО определение очень странное. Например пустое множество - это подмножество из положительных элементов, и где в нем наименьший?
Это потому что я очень внимательный, и не переписал условие, что все это только для непустых подмножеств:)
Докажите, что если упорядоченное множество

представляется как

, где

вполне упорядоченно (относительно того же порядка), а

конечно, то

вполне упорядоченно.
Как-то так? Берем минимальный элемент

в

и по очереди сравниваем его с каждым из

, что можно сделать, поскольку

конечно. Если

меньше или равно каждому элементу из

, то

минимальный элемент в

. Если найдется

такой, что

, то ищем минимальный элемент в

, что опять же, можно сделать за конечное число шагов. Тогда он и будет минимальным в

.
-- 07.08.2025, 21:32 --Хотя, видимо, то что выше, это доказательство только того, что

содержит наименьший элемент, но не каждое непустое подмножество

. Тогда нужно еще добавить, что если

и
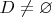
, то
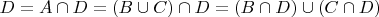
. Тогда

является подмножество

и, следовательно, содержит минимальный элемент (если не пусто), а

- подмножество

, и, следовательно, конечно. Причем, одно из них должно быть непустым. Следовательно, по тем же рассуждениям, что и выше, получаем что

содержит минимальный элемент.