Выразить случ. величину через равномерно распределенную СВ

[RikkiTan1]

Доброго времени суток!
В задачнике Ширяева по теории вероятностей в $\S 8$ есть такая задача 6.
Задача.
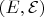
Пусть $\xi$ и $\eta$ — некоторые случайные элементы (заданные на достаточно "богатом" вероятностном пространстве) со значениями в борелевском пространстве $(E, \mathcal{E})$ (см. определение 9 в $\S$ 7 гл. II).
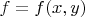
Показать, что можно найти такую измеримую функцию $f = f(x, y)$, определённую на $E \times [0, 1]$ и со значениями в $E$, и такую случайную величину $\alpha$, имеющую равномерное распределение на $[0, 1]$,
что будет выполнено представление (с вероятностью единица):

$$ \xi = f(\eta, \alpha). $$

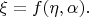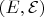
Определение 9. Измеримое пространство $(E, \mathcal{E})$ называется борелевским пространством,
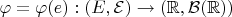
если существует взаимно однозначное отображение $\varphi=\varphi(e): (E, \mathcal{E})\to(\mathbb{R},\mathcal{B}(\mathbb{R}))$ такое, что:
1) $\varphi(E)$ есть борелевское множество;
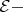
2) отображение $\varphi $ является $ \mathcal{E}-$ измеримо;
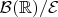
3) отображение $\varphi^{-1}$ является $\mathcal{B}(\mathbb{R})/\mathcal{E}$-измеримо;
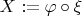
Решение: Возьмем функцию $\varphi$ из определения борелевского пространства. Тогда $X:=\varphi\circ\xi$ -- случайная величина. Пусть $F$ ее функция распределения.
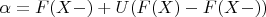
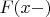
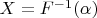
Известно, что случайная величина $\alpha= F(X-)+U(F(X)-F(X-))$, где $U$ имеет равномерное распределение и $F(x-)$ -- предел слева в точке $x$, распределена равномерно и $X=F^{-1}(\alpha)$ п.н.
Тогда $\xi=\varphi^{-1}(F^{-1}(\alpha))$.
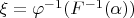
В этом решении никак не использовалась случайная величина (элемент) $\eta$. Может быть если $\eta$ не есть константа п.н., то решение можно как-то упростить?
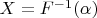
Поскольку утверждение, что $\alpha$ распределна равномерно и $X=F^{-1}(\alpha)$ п.н. не совсем тривиальные.

[mihaild]

Да вроде никак не упрощается. Возможно имелось в виду, что $\alpha$ должно быть независимо от $\eta$, или что-то подобное?

[RikkiTan1]

Ага, понятно, спасибо. Я скорее имел в виду наоборот, если $\xi$ и $\eta$ хоть как-то зависимы, то может как-нибудь через регулярные условые мат. ожидания выразить, там ведь тоже возникают функции от двух переменных.