Делимость

[maxmatem]

Дано число $A=1^{2017}+2^{2017}+3^{2017}+...+2016^{2017}$

1. доказать, что $A$ делится на $2017^2$

2. Верно ли, что $A$ делится на $2017^3$ ?

[waxtep]

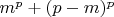
1. Для нечетного $p$ и целого $m$, $m^p+(p-m)^p$ делится на $p^2$, просто разложим бином и исследуем единственный подозрительный член $C_p^1pm^{p-1}$
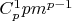
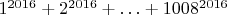
2. Нет; проверка суммы тех же подозрительных членов сводится к установлению делимости $1^{2016}+2^{2016}+\ldots+1008^{2016}$ на $2017$, но по малой теореме Ферма остаток от деления каждого слагаемого - единица

[wrest]

(Оффтоп)

Удивительно все-тки что могут бытовые гаджеты.
Планшет вычисляет сумму из задачи и затем проверяет делимость на все степени 2017 меньшие этой суммы менее чем за секунду. Гугол? Ну да, есть такое маленькое число.

? a=sum(i=1,2016,i^2017);for(i=1,2017,if(a%2017^i==0,print(i)))
1
2
time = 130 ms.

[maxmatem]

waxtep
Интересный подход ) но можно и по-другому ( пока говорить не стану )

wrest

Прогресс штука такая !

[Батороев]

maxmatem
Сначала убедиться, что $2017$ - простое число, затем вспомнить Малую теорему Ферма и в оконцовке найти $2016$-тое треугольное число.

[Null]

Батороев, по моему этого хватит только для делимости на $2017^1$

[Батороев]

Null
Я степени сослепу не углядел.
Извиняюсь!

[Dendr]

Похоже, что $F(p)=\sum\limits_{n=1}^{p-1}n^p$ всегда будет делиться на $p^2$ и никогда - на $p^3$. Для простых $p>2$.
И даже для некоторых составных нечетных.

[maxmatem]

Dendr
Вы близки !

[Руст]

Легко разложить сумму степеней $S_n^k=\sum_{i=1}^ni^k$ в сумму степеней $n$:

$$S_n^k=\frac{1}{k}\sum_{s=0}^k C_{k+1}^{k-s}B_{k-s}n^{1+s}$$

.
Так как нечетные номера чисел Бернулли равны гулю (за исключением $B_1$), получаем
делимость сумму нечетных степеней выше 1 на $n^2$, аналогично и на $(n+1)^2$.

[maxmatem]

Руст

[lel0lel]

Пусть $n\in \mathbb{N}$. Если $p$ - нечётное простое, то при $k=1,\ldots,p-1$ вычеты $k^{p^n}\bmod{p}$ различны, значит различны вычеты $k^{p^n}\bmod{p^{n+1}}$. Тогда

$$\sum\limits_{k=1}^{p-1}k^{p^n}\equiv\sum\limits_{k=1}^{p-1}g^{p^n k}\equiv 0\pmod {p^{n+1}},$$

где $g$ -- это примитивный корень $U(\mathbb {Z} /p^{n+1 }\mathbb {Z} )$