Механизм для демонстрации метода разделения переменных

[Kubrikov]

Уважаемые участники, покритикуйте пожалуйста ))

Берем две тележки, стоящие на рельсах одна над другой. К осям тележек приварены шкивы, шкивы соединены резиновым жгутом, который может предавать вращение и одновременно растягиваться. Если сдвинуть нижнюю тележку, верхняя сдвинется тоже.

Длину окружности колес тележек принимаем за 1 см, при одном обороте колеса тележка сдвинется на 1 см.

Если диаметр нижнего шкива в 4 раза больше верхнего, то нижняя тележка сдвинется на 1 см, а верхняя тележка на 4 см.

Если нижняя сдвинется еще на 1 см, верхняя передвинется уже на 8 см.

Итого:
Нижняя тележка - независимое переменное, мы ее двигаем руками, как вздумается.

Резиновые жгуты - функциональная зависимость между тележками.

Шкивы - производная: d(длина окружности верхнего шкива)/d(длина окружности нижнего шкива).

Верхняя тележка - интегрирующее устройство: проезжает столько, сколько раз провернулся ее шкив.
------------------------------------------------------------------------------
Соединим 4 тележки, как на рисунке.







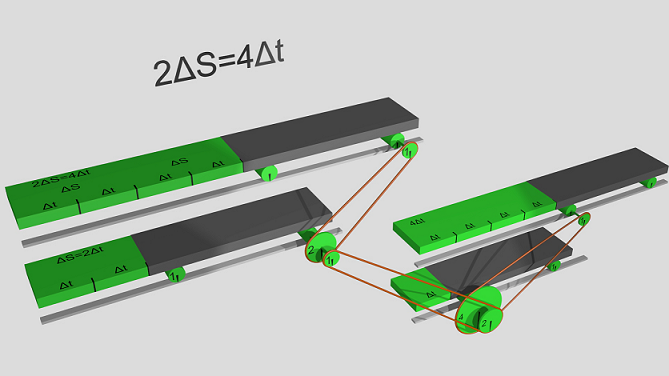
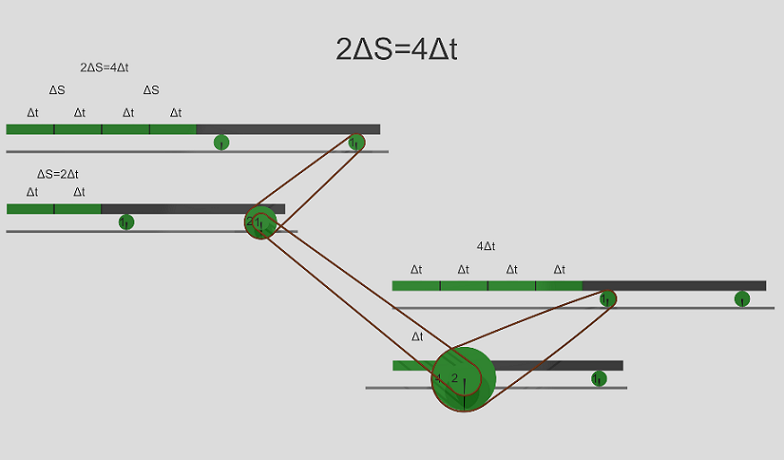
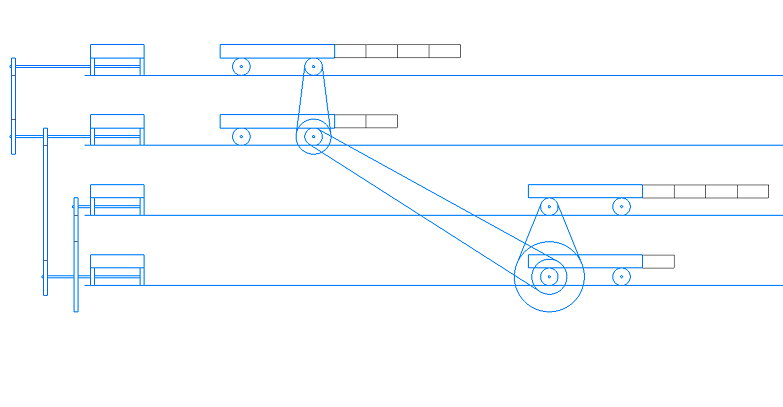
Нижняя тележка - независимое переменное; пусть это будет, например, время. Представляем время как движущуюся тележку (ничего страшного, мы же представляем время на графике как движущуюся по оси абсцисс точку).

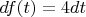
Верхняя тележка справа - реализует дифференциал $df(t)=4dt$ или интеграл, если оборотов не один.

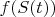
Две левых тележки реализуют сложную функцию $f(S(t))$. Где средняя тележка есть функция $S$ от $t$, а верхняя есть функция от функции от $t$.

Два последовательно соединенных жгута реализуют дифференцирование сложной функции: {df/dS\cdot dS/dt}

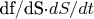
Верхняя левая тележка реализует интегрирование сложной функции: \int({df/dS\cdot dS/dt}){dt}
------------------------------------------------------------------------------
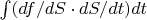
Все вместе тележки реализуют дифференциальное уравнение $2dS(t)=4dt$

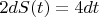
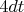
Верхние тележки перемещаются на одинаковое расстояние, в нашем случае $4dt$. Таким образом, наглядно показано равенство дифференциалов.

Если нужно решить дифференциальное уравнение относительно функции $S$, то диаметр среднего шкива нам изначально неизвестен и его надо подобрать так, чтобы соблюдалось равенство дифференциалов.


Если коэффициенты при $dS$ и $dt$ не константы, а функции, то нижний шкив должен быть ступенчатым (профиль шкива, например, в виде параболы). Жгут перекидываем по ступенькам, меняя диаметр, но это чуть позже.

Видео:

https://www.youtube.com/watch?v=cnzz8HaDk0s

https://www.youtube.com/watch?v=zZmbqGNd8DM

[Утундрий]

Подобные опусы проще разбирать с вывода.