Об уравнении y^4-1=3z^2

[Shadow]

Здравствуйте.
Недавно мне пришлось доказывать отсутствие решений в натуральных чисел уравнения $y^4-1=3z^2$. Долго мучался и справился лишь тогда, когда доказал отсутствие решений у уравнения $y^4-x^4=3z^2$ (спуском)
Есть ли попроще решение исходного уравнения, или это тот случай, когда доказать более общее утверждение легче?

Модераторам: Полные решения в данной теме приветствуются.
Спасибо.

[nnosipov]

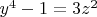
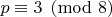
Не думаю, что есть более простое решение, чем то, которое получается методом спуска. Фактически здесь доказывается отсутствие нетривиальных решений уравнения $y^4-1=3z^2$ в рациональных числах, а это равносильно доказательству неконгруэнтности числа $3$. (Здесь $3$ можно заменить любым простым числом $p \equiv 3 \pmod{8}$, и доказательство сохранится.)

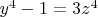
У меня была задача про более простое уравнение $y^4-1=3z^4$ (Математика в школе, 2011, № 8), но там тоже метод спуска (и читатели ее живенько так решали).

[Shadow]

Спасибо, г-н nnosipov, я знал, что вам вам будет что сказать по теме. В начале в нете поискал, ничего толкового не нашел (с формулами у меня всегда проблемы с гуглом). (Какая то опция напоследок в гугл - на любой запрос в первой очереди выдавать мысловные жемчужины ИИ по теме (не знаю как выключить!). Так вот, ИИ в очередной раз не разочаровал - объяснил, что левая часть растет быстрее, потому решений не будет.)