Существование последовательности длинной в N непростых чисел

[cxzbsdhwert]

Задача: доказать что для любого натурального $N\geq 2$ существует последовательность подряд идущих $N$ составных чисел.

3(2) дня решал, всё же решил, хотел бы привести доказательство и получить советы, подсказки, важные знания для последующего изучения Теории Чисел.

1. Обратился к тому факту, что половина чисел - чётные - непростые. Нужно как-то гарантировать "заполненность" непростыми $N$ промежутков начиная с некоторого числа.

2. Все простые, кроме 2 - нечётные.

3. Обратился к тому факту, что сумма двух чётных - чётное; двух нечётных - чётное; чётного и нечётного - нечётное.
Доказал (эти три утверждения) так: во-первых чётность - значит делимость на 2.
Нужно далее использовать теорию делимости целых чисел, а именно, что любое целое $a$ можно представить через натуральное $b$ единственным образом с целыми $q,r$, $0\leq r < b$ как: $a = bq+r$
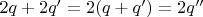
3.1 Чётное, то есть делимое на два представляется в виде $2q$. Тогда сумма чётных $2q + 2q'=2(q+q')=2q''$ тоже чётная.
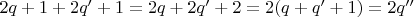
3.2 Нечётное представляется в виде суммы произведения двойки на некоторое целое и остатка. Остаток от деления на 2, если он есть (не нулевой) всегда 1 (я это понимаю, вижу, но, по крайней мере здесь не доказываю). Значит любое нечётное - $2q+1$. Тогда сумма $2q+1 + 2q' + 1=2q+2q'+2=2(q+q'+1)=2q''$ - чётное.
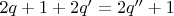
3.3 $2q+1+2q'=2q''+1$ - нечётное.

4. Просто сумма чётного и нечётного, будучи нечётным может быть простым числом, а может не быть (ну а сумма ч+ч, или н+н, будучи чётным всегда непростая).

5. Если умножить любое чётное (далее - $x$) на нечётное (далее - $y$), то будет чётное.
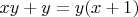
5.1 Если к произведению $xy$ добавить это же нечётное то получится гарантированная последовательность из трёх не простых, поскольку $xy$ - чётное, добавим нечётное $y$, тогда по 3.3 получим нечётное, но оно будет гарантировано составным, поскольку $xy + y = y(x+1)$. Ну а, учитывая, что оно нечётное, то двое соседей, будучи чётными, также не простые - вот и получили гарантировано 3 непростых.

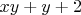
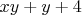
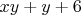
6. Дальше возникает задача с тем чтобы "накрыть", то есть гарантировать, что число не простое, числа $xy+y+2$, $xy+y+4$, $xy+y+6$ и т.д.

7. Это можно сделать, подобрав такие $x$ чётное и $y$ нечётное, чтобы их произведение было делимо как $y$, так и $y+2$ и т.д.
И вот здесь я изначально сбился с пути.
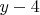
7.1 Если $a$ делит $bc$, то $a$ делит $b$ или $c$ (или обоих). Значит, нужно чтобы $y+2$ (и т.д.) делили либо чётное $x$, либо нечётное $y$. Я хорошо, заметил, что можно рассматривать наоборот - $y-2$, $y-4$ и и т.д. Очевидно, что для достаточно большого $y$, $y-2$ делить его не будет. Может какой-нибудь $y-n$ будет, но если хотя бы один, который "ближе" к $y$, например $y-2$ не будет делить, то уже нет гарантии непростого.
7.2 Значит нужно точно искать чётное $x$, которое бы было делимо $y+2$ и т.д. И вот здесь было главное упущение - я ошибочно подумал, что нечётное не делит чётное.
7.3 Ещё на этом этапе вспомнилось, что НОД делим всеми общими делителями, и что НОК делит все общие кратные, но применения этим утверждениям здесь не нашёл.

8. Дальше я решил перейти к обобщению закономерности связанной со сложением чисел разной кратности от чётности\нечётности к делимости на 2, на 3 и т.д. и попытаться имеющееся решение для последовательности из трёх изменить, используя другие кратности.

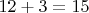
9. Потом я выписал числа от 1 до 30, выбрал в качестве произвольных чётного и нечётного 4 и 3, взял их произведение - 12. $12 + 3 = 15$, непростое, как и должно быть.

10. Дальше я заметил две ключевые вещи:
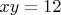
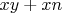
10.1 К $xy=12$ добавлять кратные $x$ или $y$ (кроме $y$ в первый раз) нет cмысла, поскольку они будут совпадать с ранее "накрытыми" числами вида $xy + xn$, и $xy +yn$.
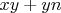
10.2 В конкретном случае который, я, к счастью, рассмотрел ($4\cdot 3=12$) - те, которые добавлять к $xy$ смысл имеют, оказались простыми.
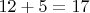
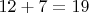
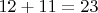
То есть $12 + 5 = 17$, $12 + 7 = 19$, $12 + 11=23$, а все остальные до них уже были накрыты тройкой, четвёркой, тройкой или четвёркой взятой несколько раз, либо до этого выбранными простыми, в том числе взятыми несколько раз.

11. Ну и дальше, фактически вернувшись к пункту 7, я совсем немного посидел в непонимании как же взять такое число, чтобы оно было кратно и одному простому и другому и третьему и т.д. пришёл к тому что их конечно же нужно было просто перемножить.

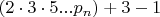
12. Тогда последовательность непростых начинается с суммы произведения нескольких идущих подряд простых и первого простого минус 1, то есть $(2\cdot 3 \cdot 5...p_n)+3-1$ (более общий случай - с произвольными простыми не знаю, будет ли работать).

Ну а доказательство существования сколько-угодно длинной такой последовательности, тогда обеспечивается бесконечностью множества простых чисел.

Зависимость между длинной последовательности и количеством задействованных в произведении простых пока не могу сформулировать, но она стремится к бесконечности, при стремлении к бесконечности количества простых.

Ну и ещё хотелось бы знать, как Вы оцениваете сложность этой задачи (на которую я потратил почти 3 дня) по 5ти бальной шкале... Ну это вообще первая решённая мной задача по теории чисел.

[nnosipov]

Хм, это, вообще говоря, очень известная задача (даже не задача, а факт). Обычно про нее пишут в самом начале параграфа про простые и составные числа в учебниках по элементарной теории чисел. Вы просто сразу не заметили простую конструкцию, хотя к ней и пришли.

Совет такой: совмещать решение задач с чтением учебников (на изобретение велосипедов времени может не хватить).

[cxzbsdhwert]

nnosipov в сообщении #1696327 писал(а):

Хм, это, вообще говоря, очень известная задача (даже не задача, а факт). Обычно про нее пишут в самом начале параграфа про простые и составные числа в учебниках по элементарной теории чисел. Вы просто сразу не заметили простую конструкцию, хотя к ней и пришли.

А если рассматривать это именно как задачу, которая была дана для самостоятельного решения в начале обучения (да, теория делимости, простые составные числа) - это всё таки я, как Вы написали "не заметил простую конструкцию", или задача неадекватно сложная для такого уровня?

nnosipov в сообщении #1696327 писал(а):

совмещать решение задач с чтением учебников (на изобретение велосипедов времени может не хватить).

Да я её в учебнике и взял.

У меня как раз наоборот ситуация - я прослушал уже 5 лекций, без практических занятий и семинаров, всё при этом понимая (хотя некоторые лекции приходилось несколько дней слушать, "перематывая" многие места по несколько раз), и в качестве контроля передоказывал, ранее понятые доказательства разных теорем, лемм, утверждений.
Но посчитал, что пусть даже самостоятельно без подсказок доказывать, то что уже ранее было доказано не достаточно для контроля, и необходимо решать "задачки", но с "задачками" оказалось как-то всё очень сложно. На математическом анализе задачи как-то по легче даются.

[Booker48]

Наверняка в OEIS (которая у меня не открывается почему-то ) есть последовательность минимальных чисел $a_n$, таких, что начиная с $a_n$ идут $n$ подряд составных.
А если минимальность не имеет значения, то $(n+1)! + 2, (n+1)! + 3, ..., (n+1)! + n + 1$ - очевидно составные.

upd Открылся OEIS
A030296

[gris]

cxzbsdhwert, кстати, интересный вариант этой задачи: доказать существование ровно N последовательных составных между двумя граничными простыми. Ну, разумеется, для нечётного N, так как вы приводили соответствующее соображение касательно чётности. Вот первые такие последовательности: [4], [8,9,10], [24, 25, 26, 27, 28]... Собственно, это легко переформулировать попроще, а насчёт доказать не уверен
OEIS открылась и показала несколько первых примеров.
Кстати, в усложнённых рассуждениях ТС есть смысл: пригодятся для других задач

[mihaild]

A100964$(n)$ - минимальное число, после которого гэп $2n$.

gris в сообщении #1696333 писал(а):

Кстати, интересный вариант этой задачи: доказать существование ровно N последовательных составных между двумя граничными простыми

А это A000230. И определена ли она для всех $n$ - открытый вопрос. Собственно есть более сильное утверждение - гипотеза Полиньяка: любой гэп встречается бесконечное число раз. И более слабое - любое четное число есть разность двух простых (не обязательно идущих подряд). Поскольку истинность обоих открытый вопрос, то ответ на ваш вопрос - любой ли гэп реализуется - мы не найдём.

cxzbsdhwert
Но кстати по мотивам вышесказанного - вот Вам посильная задачка. Есть 168 простых, меньших тысячи. Докажите, что существует миллион идущих подряд чисел, среди которых ровно $42$ простых.

[cxzbsdhwert]

mihaild в сообщении #1696334 писал(а):

A100964$(n)$ - минимальное число, после которого гэп $2n$.

gris в сообщении #1696333 писал(а):

Кстати, интересный вариант этой задачи: доказать существование ровно N последовательных составных между двумя граничными простыми

А это A000230. И определена ли она для всех $n$ - открытый вопрос. Собственно есть более сильное утверждение - гипотеза Полиньяка: любой гэп встречается бесконечное число раз. И более слабое - любое четное число есть разность двух простых (не обязательно идущих подряд). Поскольку истинность обоих открытый вопрос, то ответ на ваш вопрос - любой ли гэп реализуется - мы не найдём.

cxzbsdhwert
Но кстати по мотивам вышесказанного - вот Вам посильная задачка. Есть 168 простых, меньших тысячи. Докажите, что существует миллион идущих подряд чисел, среди которых ровно $42$ простых.

Это точно задачи, которые даются на самостоятельное решение в самом начале изучения? Пусть даже для каких-то самых сложных образовательных программ

-- 04.08.2025, 17:52 --

gris в сообщении #1696333 писал(а):

cxzbsdhwert, кстати, интересный вариант этой задачи: доказать существование ровно N последовательных составных между двумя граничными простыми. Ну, разумеется, для нечётного N, так как вы приводили соответствующее соображение касательно чётности. Вот первые такие последовательности: [4], [8,9,10], [24, 25, 26, 27, 28]... Собственно, это легко переформулировать попроще, а насчёт доказать не уверен
OEIS открылась и показала несколько первых примеров.
Кстати, в усложнённых рассуждениях ТС есть смысл: пригодятся для других задач

Подразумевается, что это может решить первокурсник пусть даже специалитета на первых занятиях (семинарах)? Решить именно, не знать такой факт, и просто его применить, а именно сам решить?

[mihaild]

cxzbsdhwert в сообщении #1696336 писал(а):

Это точно задачи, которые даются на самостоятельное решение в самом начале изучения?

Мою задачу - да, я бы ожидал, что сильный школьник решит.
А вот задачу gris - нет, её решения на текущий момент не знает вообще никто в мире

[Shadow]

cxzbsdhwert в сообщении #1696325 писал(а):

Ну а доказательство существования сколько-угодно длинной такой последовательности, тогда обеспечивается бесконечностью множества простых чисел.

Бесконечность простых чисел как раз затрудняет решение задачи. Нет?

[cxzbsdhwert]

Shadow в сообщении #1696339 писал(а):

cxzbsdhwert в сообщении #1696325 писал(а):

Ну а доказательство существования сколько-угодно длинной такой последовательности, тогда обеспечивается бесконечностью множества простых чисел.

Бесконечность простых чисел как раз затрудняет решение задачи. Нет?

Ну, если есть необходимость в доказывании, то это усложняет. А если использовать, полагая истинным, на основании доказывания ранее - то нет.
А вообще, насколько я понял, перемножать можно (или даже нужно) было не только простые но и просто $y+2$, $y+4$, и т.д., или даже вообще просто факториал брать, поэтому доказывать бесконечность простых вообще не нужно.

[wrest]

cxzbsdhwert в сообщении #1696340 писал(а):

или даже вообще просто факториал брать, поэтому доказывать бесконечность простых вообще не нужно.

Ну да, тут вроде чрезвычайно просто, и главное -- конструктивно. Можно немедленно предъявить $N$ последовательно идущих составных чисел, указав на первое из них $(N+1)!+2$ без всяких предположений о распределении простых чисел.

[cxzbsdhwert]

cxzbsdhwert в сообщении #1696325 писал(а):

7.1 Если $a$ делит $bc$, то $a$ делит $b$ или $c$ (или обоих)

А это же не верное, точнее не всегда верное утверждение: $25|5\cdot 10$, но 25 не делит ни 5 ни 10.