Несобственный интеграл и пространство функций?

[Divergence]

Есть интеграл от функции для функции $f(x) \in C[a,b]$, где $[a,b]$ конечный интеграл на вещественной оси

$$ \int^u_a |x|^{p-1} \, f(x) \, dx , $$

где $p \in (0,1]$ $u \in (a,b]$.

Если $a<0<b$, то этот интеграл будет несобственным интегралом второго рода, поскольку подинтегральное выражение неограничено в точке $x=0$.

Как обычно обозначается пространство фунций (подпространство $C[a,b]$), для которых этот интеграл существует?
Существуют ли общепринятые обозначения типа $C_{0}[a,b]$ или $C_{p-1}[a,b]$ ?

[Combat Zone]

Не очень понятен вопрос. Вы хотите организовать пространство для подынтегральных функций, или вопрос касается только в каком пространстве должны функции $f$ лежать?

[Divergence]

Вопрос касается только в каком пространстве должны функции $f$ лежать?

[Combat Zone]

Ну вы уже потребовали от них непрерывности. Этого достаточно.
В тех случаях, когда интеграл будет несобственным, он будет абсолютно сходящимся. Чего же лучше?

[Divergence]

Спасибо за комментарий.

То есть несмотря на неограниченность подинтегрального выражение на интервале $[a,b]$,
для абсолютной сходимости доcтаточно непрерывности подинтегрального выраженияна $[a,0) \cup (0,b]$ ?

В какой книге на русском или английском можно прочитать теорему такото типа, в идеале с доказательством.

-- 03.08.2025, 12:59 --

Для написанного подинтегрального выражения ведь важно что $p \in (0,1]$ илия не прав.

[Combat Zone]

Divergence в сообщении #1696228 писал(а):

Для написанного подинтегрального выражения ведь важно что $p \in (0,1]$ илия не прав.

Если не накладывать дополнительных ограничений на значения $f$ в нуле - то да. Для доказательства достаточно любого признака сравнения для несобственных интегралов второго рода, излагаемого в курсе анализа (высшей математики). Самые стандартные учебники.
Из непрерывности следует ограниченность.

-- 03.08.2025, 12:18 --

Divergence в сообщении #1696228 писал(а):

для абсолютной сходимости доcтаточно непрерывности подинтегрального выраженияна $[a,0) \cup (0,b]$ ?

Недостаточно. Но вы и не об этом хотели говорить. Вы хотели говорить о непрерывности $f$ на отрезке $[a,b]$. Это очень сильное условие, его можно как-то ослабить, но у вас непрерывность есть исходно. Так зачем от нее отказываться?

[Divergence]

Спасибо.
То есть получается типо следующего.

Есть Теорема (Mean value theorems for definite integrals):
В общем случае, если $f(x) \in C[a, b]$, $[a, b] \subset \mathbb{R}$ непрерывна и $g(x)$ — интегрируемая функция, не меняющая знак на $[a, b]$, то существует число $c \in (a, b)$ такое, что

$$ \int^{b}_{a} f(x) \, g(x) \, dx \, = \, f(c) \, \int^{b}_{a} g(x) \, dx. $$

В моем случае $g(x) = |x|^{p-1}$ и поэтому

$$ \int^{b}_{a} f(x) \, g(x) \, dx \, = \, f(c) \, \int^{b}_{a} |x|^{p-1} \, dx \, = \, f(c) \ \frac{1}{p} (b^p-a^p)< \infty $$

при любых $a,b \in \mathbb{R}$, $a<b$, так как $p \in (0,1]$.

[Combat Zone]

Divergence
Ваша $g$ на вашем отрезке не является интегрируемой по Риману, а теоремы о среднем (обе) ничего другого не понимают.
Прочитайте признак сравнения (тот, где неравенства) для несобственных интегралов.
Поскольку $f$ непрерывна на отрезке $[a,b]$, она ограниченна на нем, следовательно при $ 0 < p < 1$
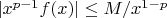
$|x^{p-1}f (x)| \le M/x^{1-p}$, интеграл от большей функции сходится (показатель в знаменателе меньше единицы), значит, от меньшей тем более сходится.

В стартовом посте у вас интеграл не по всему отрезку, а с переменным верхним пределом, так что это функция, но раз уж вы решили не обращать на это внимание, то и я не стану. То есть, если вы читаете какую-то книжку, контекст может быть несколько иным.

[Divergence]

Спасибо.