В таком случае нужно доказать, что для любой точки
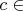
O\cap\mathbb{I}

существует последовательность
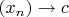
, и при этом
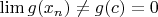
.
Как вариант, можно взять последовательность рациональных
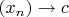
. Тогда
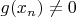
для любого

. Но ведь этого же недостаточно, чтобы утверждать, что
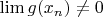
. В общем, прошу еще одну подсказку:)
Я думаю, проще использовать результат вашей предыдущей задачи о непрерывности расстояния от точки до множества.
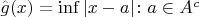
непрерывна на множестве

(которое у вас

, мне обозначения не нравятся. Точка

мне не нравится тоже, она народ с толку сбивает, путаясь с обозначением дополнения, пусть будет

).
А дальше без разницы, какое

, рациональное или иррациональное. Проблему представляют только те, что лежат в

.
Множество иррациональных всюду плотно, так что найдется последовательность, сходящаяся к

, на этой последовательности функция нулевая. Множество рациональных всюду плотно, и тоже найдется последовательность, сходящаяся к

, на ней функция будет равна расстоянию до множества, а оно непрерывно, и под его знаком можно переходить к пределу. Осталось сравнить и сделать выводы.
Открытость используется, расстояние от точки

до дополнения должно быть строго положительно.
Поскольку

открытое, то существует

такое что
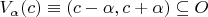
.
Тогда для любого
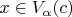
:
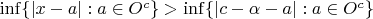
(или
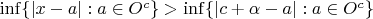
).
В любом случае, для
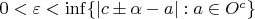
для любого

найдется такой рациональный
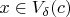
, что
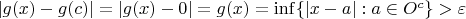
.
Сейчас вчитаюсь. Свои мысли проще думать.
Upd. Нормально. Немного тяжеловесно на мой взгляд, но это вкусовщина.