Примем следующее обозначение:
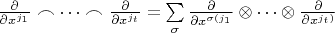
, где сумма берется по всем перестановкам индексов. Теперь определим (по Геометрическим методам Катанаева) симметричное тензорное произведение симметричных контравариантных тензоров

порядка

и

порядка

:
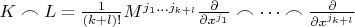
,
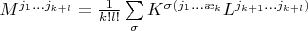
,
а также скобку Схоутена:
![$[K,L]^{j_1 \dots j_{k+l-1}} = \frac{1}{(k+l-1)!}(\sum\limits_{\sigma}^{}kK^{i\sigma (j_1 \dots j_{k-1}}\frac{\partial L^{j_k \dots j_{k+l-1})}}{\partial x^i} - \sum\limits_{\sigma}^{}lL^{i\sigma (j_1 \dots j_{l-1}}\frac{\partial L^{j_l \dots j_{k+l-1})}}{\partial x^n})$ $[K,L]^{j_1 \dots j_{k+l-1}} = \frac{1}{(k+l-1)!}(\sum\limits_{\sigma}^{}kK^{i\sigma (j_1 \dots j_{k-1}}\frac{\partial L^{j_k \dots j_{k+l-1})}}{\partial x^i} - \sum\limits_{\sigma}^{}lL^{i\sigma (j_1 \dots j_{l-1}}\frac{\partial L^{j_l \dots j_{k+l-1})}}{\partial x^n})$](https://dxdy-04.korotkov.co.uk/f/f/0/e/f0e8c6de995b45d30e745401ad35b3d882.png)
.
Определение скобки Схоутена вроде специально такое, что должно быть выполнено тождество:
![$[T \frown K, L] = [T,L] \frown K + T \frown [K,L]$ $[T \frown K, L] = [T,L] \frown K + T \frown [K,L]$](https://dxdy-02.korotkov.co.uk/f/1/2/2/12250b37d2d57bdeab82231b9d43987382.png)
.
Я его хочу доказать по индукции по

для двух случаев - первый для
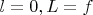
и второй для

, но у меня почему-то не выходит равенство в обоих случаях при
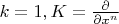
.
Вот например для начала попробуем доказать, что
![$[T\frown \frac{\partial}{\partial x^n}, f] = [T,f] \frown \frac{\partial}{\partial x^n}+ T \frown [\frac{\partial}{\partial x^n},f]$ $[T\frown \frac{\partial}{\partial x^n}, f] = [T,f] \frown \frac{\partial}{\partial x^n}+ T \frown [\frac{\partial}{\partial x^n},f]$](https://dxdy-02.korotkov.co.uk/f/d/5/6/d56c7c576f38aef36f4146204651f5f882.png)
:
![$[T\frown \frac{\partial}{\partial x^n}, f]^{j_1 \dots j_t}=(t+1)(T \frown \frac{\partial}{\partial x^n})^{j_1 \dots j_t i} \frac{\partial f}{\partial x^i}$ $[T\frown \frac{\partial}{\partial x^n}, f]^{j_1 \dots j_t}=(t+1)(T \frown \frac{\partial}{\partial x^n})^{j_1 \dots j_t i} \frac{\partial f}{\partial x^i}$](https://dxdy-01.korotkov.co.uk/f/8/2/9/829af5d80e3ba7a18352c88984af57fd82.png)
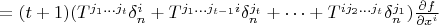
,
![$([T,f] \frown \frac{\partial}{\partial x^n})^{j_1 \dots j_t} = ([T,f]^{j_1 \dots j_{t-1}}\delta ^{j_t}_n + \dots + [T,f]^{j_2 \dots j_{t}}\delta ^{j_1}_n)$ $([T,f] \frown \frac{\partial}{\partial x^n})^{j_1 \dots j_t} = ([T,f]^{j_1 \dots j_{t-1}}\delta ^{j_t}_n + \dots + [T,f]^{j_2 \dots j_{t}}\delta ^{j_1}_n)$](https://dxdy-02.korotkov.co.uk/f/1/d/7/1d7d53b3a4553377a3785ba5634d376782.png)
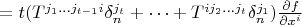
,
![$(T \frown [\frac{\partial}{\partial x^n},f])^{j_1 \dots j_t} = T^{j_1 \dots j_t}\frac{\partial f}{\partial x^n}$ $(T \frown [\frac{\partial}{\partial x^n},f])^{j_1 \dots j_t} = T^{j_1 \dots j_t}\frac{\partial f}{\partial x^n}$](https://dxdy-01.korotkov.co.uk/f/8/5/4/8542d9fd7060998f540fc9bbb675201c82.png)
.
Получается, что у меня возникают лишние коэффициенты

и

и тождество не работает, почему так получается я вообще не вижу, видимо где-то делаю ошибку, но где именно?