Задача. Пусть
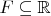
- замкнутое множество. Определим
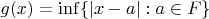
. Показать, что

непрерывна на всех вещественных числах.
Решение. Покажем, что

непрерывна в произвольной точке

.
Поскольку множество  замкнуто, то найдется такая точка
замкнуто, то найдется такая точка 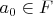 , что
, что 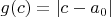 (то есть,
(то есть, 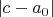 минимально).
минимально). Тогда для любого

имеем
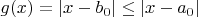
, где
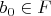
.
Пусть
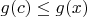
. Тогда
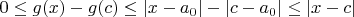
. Последнее неравенство следует из обратного неравенства треугольника.
Пусть
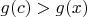
. Тогда
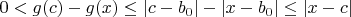
.
Таким образом,
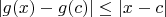
. Тогда для любого

существует

, такая что если

, то
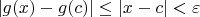
, что и есть определение непрерывности.
Вопрос 1. Есть непонятный момент в доказательстве (выделил жирным). Моя попытка ниже, но до конца что-то не могу докрутить. Возможно, ушел вообще не в ту степь.
От противного, предположим, что для любого

существует
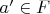
, такое что
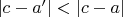
. Тогда можно построить убывающую последовательность
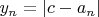
, где все
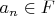
. Поскольку она ограничена снизу (нулем), то последовательность сходится. Пусть
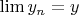
.
Последовательность
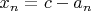
ограничена, поскольку
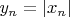
, а

ограничена. Следовательно, по теореме Больцано-Вейерштрасса, можно выделить сходящуюся подпоследовательность
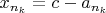
. Тогда
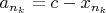
сходится.
Дальше, по идее нужно доказать, что
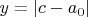
, где
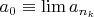
, и тогда, поскольку

замкнуто,
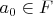
, что противоречило бы изначальному предположению. Но что-то не пойму, как это сделать. Есть теорема, что если
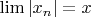
и при этом последовательность

не содержит подпоследовательностей, сходящихся к

, то

. Возможно, нужно как-то использовать ее, но пока не особо получается.
Вопрос 2. Если принять, что выделенное утверждение справедливо, то правильна ли остальная часть доказательства?