Как вычислять градиент для векторного выражения?

[Kevsh]

Столкнулся с таким выражением:

$$\xi=E[d^2]+W^TRW-2P^TW,$$

при этом W - вектор, P - вектор, R - матрица. Теперь мы хотим вычислить градиент:

$$\nabla=\frac{\partial\xi}{\partial W}=[\frac{\partial\xi}{\partial w_0} \text{ } \frac{\partial\xi}{\partial w_1} \text{ } ... \text{ } \frac{\partial\xi}{\partial w_L}]^T=2RW-2P$$

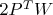
Вот я совершенно не понимаю, как вообще вычислять этот градиент. Третье слагаемое ещё более-менее понятно, только не очень ясно, куда в $2P^TW$ теряется транспонирование. Первое слагаемое понятно - от $W$ не зависит, значит производные равны нулю. Второе - вообще ноль понимания. Мне кажется я чего-то фундаментально не понимаю, но я с таким впервые сталкиваюсь...

[mihaild]

А попробуйте честно расписать матричное умножение, через элементы матрицы.