Справа, то что должно получиться, слева - что получилось при обратном преобразовании Фурье
Очевидно, что вы что-то напутали и обратное преобразование не соответствует прямому (один оператор не является обратным ко второму). Попробуйте построить матрицу прямого преобразования (БПФ — это линейное преобразование, его можно записать в матричном виде), обратить её в лоб (для какого-нибудь разумно малого размера данных) и сравнить результат с тем, что вы делаете при обращении по формуле (записав это обращение тоже в матричной форме).
Можно ли как выразить коэффициент разложения
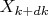
(
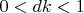
) несобственной функции
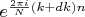
через коэффициенты разложения двух соседних собственных
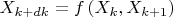
Если я правильно понял вопрос, то вот эта статья обсуждает его в одномерном случае:
Eric Jacobsen and Peter Kootsookos - Fast, Accurate Frequency Estimators. Однако, это всё от лукавого. В реальности шумы и/или другие частотные компоненты, которые не попадают на гребёнку БПФ могут заметно сместить оценку частоты. Чем ближе к друг другу частотные компоненты, тем сильнее смещение. Даже для чистого синусоидального сигнала результат может зависеть от того, как он сфазирован относительно прямоугольного окна. Поэтому лучше использовать окна типа
окно Ганна или окно flap-top, у которых на краях и сама оконная функция и её производная нулевые. Далее, реальные сигналы как правило имеют амплитудную и частотную модуляцию. В этом случае уточнение частоты вообще смысл теряет, потому что в разные моменты времени она может быть разная. Надеюсь, мой ответ поможет хоть как-то.