DedekindЯ чего-то не понимаю, или Ваш вопрос сводится к "можно ли ввести структуру группы на множестве континуальной мощности"? Очевидно, можно, причем бесконечным количеством способов (самый очевидный уже подсказали). Или у Вас есть особые пожелания к групповой операции?
Может быть, Вы хотите определить умножение

на

так, чтобы оно "почти нигде" не отличалось от обычного умножения вещественных чисел

? Т.е. существует иррациональная единица

, но
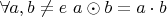
? Если Вы хотите именно этого, то не получится.