Хочу найти скачок теплоемкости в модели БКШ. Считаю энергию квазичастичных возбуждений при
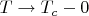
:
![$$ E(T,\Delta(T)) = \frac{g_F}{2} 2 \int\limits_{0}^{\infty} d\xi \frac{\sqrt{\xi^2 + \Delta^2}}{e^{\frac{\sqrt{\xi^2+\Delta^2}}{T}}+1} = [\xi = Tx, \Delta = T u]=\frac{mVp_F}{\pi^2} T^2 \int\limits_{0}^{\infty} dx \frac{\sqrt{x^2+u^2}}{e^{\sqrt{x^2+u^2}}+1} \equiv \frac{mVp_F}{\pi^2}T^2 J(u)$$ $$ E(T,\Delta(T)) = \frac{g_F}{2} 2 \int\limits_{0}^{\infty} d\xi \frac{\sqrt{\xi^2 + \Delta^2}}{e^{\frac{\sqrt{\xi^2+\Delta^2}}{T}}+1} = [\xi = Tx, \Delta = T u]=\frac{mVp_F}{\pi^2} T^2 \int\limits_{0}^{\infty} dx \frac{\sqrt{x^2+u^2}}{e^{\sqrt{x^2+u^2}}+1} \equiv \frac{mVp_F}{\pi^2}T^2 J(u)$$](https://dxdy-01.korotkov.co.uk/f/c/1/5/c1568199be658becb9338fcc54c8bb8282.png)
Здесь верхний предел интегрирования был выставлен бесконечностью, а не

, т.к.
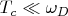
.
Итак, задача свелась к нахождению асимптотики интеграла

при
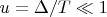
. Заметим, что:
![$$J(u) = \frac{1}{2}\int\limits_{0}^{\infty} dx \sqrt{x^2 + u^2} \left[1-\th\left(\frac{\sqrt{x^2+u^2}}{2}\right)\right] \equiv \frac{J_1(u) + J_2(u)}{2}$$ $$J(u) = \frac{1}{2}\int\limits_{0}^{\infty} dx \sqrt{x^2 + u^2} \left[1-\th\left(\frac{\sqrt{x^2+u^2}}{2}\right)\right] \equiv \frac{J_1(u) + J_2(u)}{2}$$](https://dxdy-02.korotkov.co.uk/f/d/3/6/d361ba607499040c2989e144a01b8de182.png)
Здесь:
![$$J_1(u) \equiv \int\limits_{0}^{\infty} dx \left(\sqrt{x^2+u^2} - x\th{\frac{x}{2}}\right) = \left[\frac{1}{2}x \sqrt{u^2 + x^2} + u^2 \tanh^{-1}{\left(\frac{x}{\sqrt{u^2+x^2}}\right)} -\frac{x^2}{2} \th{\frac{x}{2}}\right] \bigg{|}^{\infty} + $$ $$J_1(u) \equiv \int\limits_{0}^{\infty} dx \left(\sqrt{x^2+u^2} - x\th{\frac{x}{2}}\right) = \left[\frac{1}{2}x \sqrt{u^2 + x^2} + u^2 \tanh^{-1}{\left(\frac{x}{\sqrt{u^2+x^2}}\right)} -\frac{x^2}{2} \th{\frac{x}{2}}\right] \bigg{|}^{\infty} + $$](https://dxdy-01.korotkov.co.uk/f/0/6/e/06e6200a0604704281e923f20a42fc2582.png)
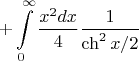
Здесь
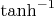
- гиперболический арктангенс. Первый член был проинтегрирован в лоб, второй - по частям. Упрощая, получим:
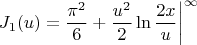
Полученная логарифмическая расходимость сократится вторым интегралом, который определяется как:
![$$J_2(u) \equiv \int\limits_{0}^{\infty} \left[x\th{\frac{x}{2}} - \sqrt{x^2+u^2} \th{\frac{\sqrt{x^2+u^2}}{2}}\right] $$ $$J_2(u) \equiv \int\limits_{0}^{\infty} \left[x\th{\frac{x}{2}} - \sqrt{x^2+u^2} \th{\frac{\sqrt{x^2+u^2}}{2}}\right] $$](https://dxdy-01.korotkov.co.uk/f/8/0/8/808a8d60ac805a017098b99c471af31682.png)
Его придется считать приближенно в пределе
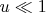
:
![$$J_2(u) \approx -\frac{u^2}{2} \int\limits_{0}^{\infty} \frac{dx}{x} \left(x\th{\frac{x}{2}}\right)'=-\frac{u^2}{2}\left[\int\limits_{0}^{\infty} \frac{dx}{x}\th{\frac{x}{2}} + \frac{1}{2}\int\limits_{0}^{\infty} dx \frac{1}{\ch^2{(x/2)}}\right] =$$ $$J_2(u) \approx -\frac{u^2}{2} \int\limits_{0}^{\infty} \frac{dx}{x} \left(x\th{\frac{x}{2}}\right)'=-\frac{u^2}{2}\left[\int\limits_{0}^{\infty} \frac{dx}{x}\th{\frac{x}{2}} + \frac{1}{2}\int\limits_{0}^{\infty} dx \frac{1}{\ch^2{(x/2)}}\right] =$$](https://dxdy-02.korotkov.co.uk/f/1/4/1/14189cd882d7b2e6a5de51c1cede930182.png)
![$$= -\frac{u^2}{2} \left[\ln{x}\th{\frac{x}{2}} \bigg{|}^{\infty} - \int\limits_{0}^{\infty} \frac{\ln{x}dx}{2\ch^2{(x/2)}}+1\right]= -\frac{u^2}{2} \left[\ln{x}\bigg{|}^{\infty} - \ln{\frac{\pi}{2\gamma}}+1\right]$$ $$= -\frac{u^2}{2} \left[\ln{x}\th{\frac{x}{2}} \bigg{|}^{\infty} - \int\limits_{0}^{\infty} \frac{\ln{x}dx}{2\ch^2{(x/2)}}+1\right]= -\frac{u^2}{2} \left[\ln{x}\bigg{|}^{\infty} - \ln{\frac{\pi}{2\gamma}}+1\right]$$](https://dxdy-03.korotkov.co.uk/f/2/2/d/22d045ee7b9fcc47784ee6d4199335c982.png)
Здесь
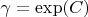
, где
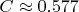
- постоянная Эйлера Маскерони.
Суммируя интегралы

, получим окончательно:
![$$J(u) \approx \frac{\pi^2}{12} + \frac{u^2}{4} \left[\ln{\frac{\pi}{\gamma u}} - 1\right], u \ll 1$$ $$J(u) \approx \frac{\pi^2}{12} + \frac{u^2}{4} \left[\ln{\frac{\pi}{\gamma u}} - 1\right], u \ll 1$$](https://dxdy-01.korotkov.co.uk/f/8/a/7/8a7616ecf8599addda7c5891b21620ae82.png)
Построил в Mathematica - не очень уверенно асимптотика совпадает с интегралом. Так что первый вопрос -
верна ли эта асимптотика?
Что мне не нравится - то что для энергии я получаю:
![$$E(T,\Delta(T)) \approx E(T,0) + \frac{mVp_F}{4\pi^2} \Delta^2 \left[\ln{\frac{\pi T}{\gamma \Delta}} - 1\right]$$ $$E(T,\Delta(T)) \approx E(T,0) + \frac{mVp_F}{4\pi^2} \Delta^2 \left[\ln{\frac{\pi T}{\gamma \Delta}} - 1\right]$$](https://dxdy-02.korotkov.co.uk/f/1/c/5/1c59c969b252a95a2e0bc65eb9f63a9982.png)
Учивая, что
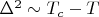
, имеем функцию вида
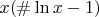
по переменной
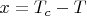
, и эта функция не имеет конечной производной при

, то есть скачок теплоемкости бесконечен, что неверно.
Так что второй вопрос:
что я сделал не так и содержится ли проблема в вычислении асимптотики интеграла или в чем-то другом?