Изучая диофантовые уравнения обнаружил что очень малое количество авторов и материала в интернете связанный с этой областью. Может действительно все связано с очень сложными оссобенностями решения таких уравнений?
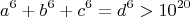
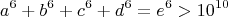
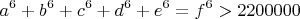
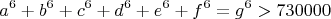
Упоминая про первые два уравнения впринципе не видел нигде. Все что известно на сегодняшний в пределах вычеслений было проверено, очень большое количество диапозонов, но пока не обнаружено никаких примеров. Может возможно доказать, что решения есть хотябы для последних двух уравнений? Что весьма интересно некоторые уравнения образуют весьма причудливые спорадические группы решений.
Возможные идеи и факты:
если воспользоваться равенством для суммы трёх кубов

можно получить весьма интересную параметризацию дающая сразу два параметра с 6 степенями.
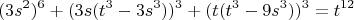
После чего можно сделать замену
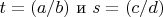
![$$
И приравнять второй [math]$3s(t^3-3s^3)=\dfrac{x^2}{b^4}$$ $$
И приравнять второй [math]$3s(t^3-3s^3)=\dfrac{x^2}{b^4}$$](https://dxdy-02.korotkov.co.uk/f/1/2/0/1203a5c258d42400a2a59e3355373ac282.png)
[/math]
Код написанный на коленях выдаёт очень много решений; но в пределах 25000 есть только одно спорадические решение завязанное на
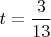
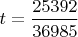
... ринг:
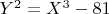
a;b;c;d→

→
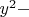
приближение:
1;1;3;13;138;159.380
1;1;6;26;552;637.520
1;1;9;39;1242;1434.420
....
2;1;60;130;55200;63752.020
2;1;66;143;66792;77139.944
2;2;3;13;552;637.520
...
8;1;24;13;8832;10200.323
8;1;48;26;35328;40801.293
8;1;72;39;79488;91802.908
8;2;12;13;8832;10200.323
8;2;24;26;35328;40801.293
8;2;36;39;79488;91802.908
8;2;48;52;141312;163205.170
8;2;60;65;220800;255008.078
8;2;72;78;317952;367211.633
8;2;84;91;432768;499815.833
8;3;8;13;8832;10200.323
8;3;16;26;35328;40801.293
...
Но в основном параметризации играет в роли такая формула, возможно можно получить более подробную формулу, если кто знает как можно вытянуть из этого уравнения
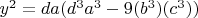
какую либо параметризацию ?
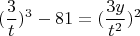
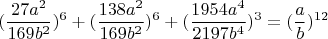
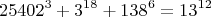
вообщем из неё никак из других спорадических формул решения особо не вытянешь. Можно в целом попытаться решить вот такое уравнение:
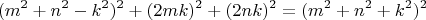
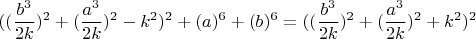
И чтобы продолжить надо решить оба уравнения:
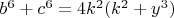
и
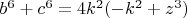
как это сделать тоже трудно представляю возможным, но если кто знает может помочь, где то на форуме видел уравнение Рахими если кто сможет это привести к виду уравнения Рахими с параметризацией буду благодарен.
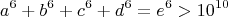
Насчёт остальных уравнений есть пара интересных параметризаций. Но все таки большинство из них подчиняется правилу бессконечного квадрата квадратов.
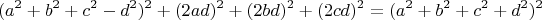
Всегда остаётся два слагаемых которые нужно привести к форме кубов.
Есть другая специфичная параметризация на кубы, увидел в одном математическом сборнике:
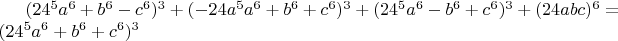
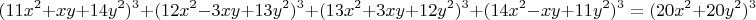
.
И ещё их достаточно много, можно вкладывать меньшую в большую.
Для:
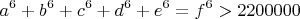
Данного уравнения самая большая надежда поскольку нашли очень хорошую линейную параметризацию которая не используют все множители подряд хотя сомнения по сложности вызывает:
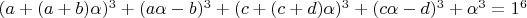
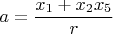
,
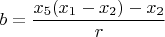
,
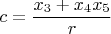
,
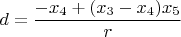
,
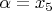
,
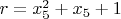
В общей сложности нужно преобразовать минимум 4 коэффициента.
Для последнего уравнения чего-то использующиего кубы не видел.
Хотя вероятно что скоро его могут найти.