Запутался в комбинаторной задаче

[ukatan]

Здравствуйте.
Запутался я в комбинаторной задаче. Вот два варианта задачи имеющей одинаковый алгоритм решения, а найти его не могу.

Задача №1
Входные данные:
Есть 5 филиалов завода и на общегодовое собрание было решено отправить по 2 представителя из каждого филиала. Для них в комнате совещаний был установлен круглый стол и 10 стульев.
Пары представителй прибывают на совещание с интервалом 5-10 минут. Сколько есть вариантов рассадить пары представителей на стулья? Порядок не важен, и какие они будут занимать свободные стулья, тоже не важно.

Мои размышления:
Тяяк, 5 пар и 10 стульев, уже хорошо, места хватит всем. Пишла первая пара, она может занять любые два стула, а значит это сочетания без повторений. И так можно посчитать для каждой пары, ну кроме последней, а потом просто перемножить результаты. Но это не очень удобно, особенно если филиалов не 5, а 10, 20, 100, 1000. Не могу придумать как можно это посчитать не перемножая 999 множителей.

Задача №2
Входные данные:
В клуб знакомств пришли 5 мужчин и 5 женщин, сколько есть вариантов создать 5 пар?

Мои размышления:
Ну 5 на 5 будет 5, это-то понятно, а дальше опять, как и в предыдущей задаче. Сочетания без повторений для первой пары, второй, третей, четвертой и потом перемножить. И опять та же проблема. А если придёт 1000 мужчин и 1000 женщин? Опять выписывать на бумажку 999 результатов, а потом их перемножать это не выход.

Должен же быть какой-то способ более красивого решения таких задач. В какую сторону думать?

[Yadryara]

ukatan в сообщении #1695184 писал(а):

Должен же быть какой-то способ более красивого решения таких задач.

Слово-то есть красивое. И даже значок есть поблизости: между и .

[ukatan]

Yadryara в сообщении #1695186 писал(а):

Слово-то есть красивое. И даже значок есть поблизости

Тонко
Спасибо, сейчас попробую прикинуть как это "красивое" слово может помочь. Только тогда получается, если исользовать для второй задачи "красивое" слово, то эти две задачи имеют разные алгоритмы решения.

[dgwuqtj]

ukatan в сообщении #1695191 писал(а):

Только тогда получается, если исользовать для второй задачи "красивое" слово, то эти две задачи имеют разные алгоритмы решения.

Так для первой задачи это слово тоже можно использовать. И это более элементарная тема, чем сочетания без повторений.

[ukatan]

Спасибо всем за помощь!
Разобрался.
Ё-моё, это же "первый класс, вторая четверть", а я уже несколько дней ломал голову как придумать красивое решение для задачи №1. А сбила меня с толку блок-схема, "как выбрать формулу комбинаторики". А в ней первым пунктом идёт вопрос: "Порядок важен?" Нет? Значит это сочетания. Я упёрся в это и стал притягивать решение задачи №1 к сочетаниям ничего не замечая вокруг. Хотя раз 15-20 читал пример про 3 книжки с полки и там можно было рассмотреть подсказку.
Что касается задачи №2, то из-за того, что запарился первой задачей и зациклился на сочетаниях без повторений, то увидев похожие данные, сразу определил её в сочетания.
Завтра постараюсь более подробно описать ход мыслей.

[ukatan]

Как и обещал ход мыслей:
После того как Yadryara показал направление, я решил отложить свои многодневные думки и взглянуть на задачи под другим углом.
Взял задачу №2 и стал рассуждать: пришли 5 мужчин и 5 женщин, значит первая женщина может выбрать любого мужчину пятью способами, вторая уже четырьмя и т.д.
Следовательно общее количество пар будет $5 \cdot 4 \cdot 3 \cdot 2$ Так это же и есть "красивое" слово.
На радостях накинулся с факториалом на первую задачу и... Что-то пошло не так.
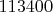
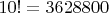
Вместо ответа $113400$ я получил $10! =3628800 $. Интересно, а если 10! разделить на правильный ответ? $3628800 : 113400 = 32$. Ну 32 и что? Хотя число очень знакомое, да это же степень двойки. $2^5=32$
Интересное совпадение, степень пятая и пар представителей тоже пять.
dgwuqtj подсказал, что через "красивое" слово первая задача будет иметь более изящное решение, чем с помощью сочетаний. Да и Yadryara намекал на "красивое" слово.
Надо $2^5$ как-то прикрутить к факториалу,хм. Решил расписать задачу на бумаге. Пришла первая пара представителей, один из них может занять стул 10-ю способами, другой уже 9-ю, значит пара может занять стулья $10 \cdot 9 = 90$ способами. Но это получилась упорядоченная выборка, а нужна неупорядоченная выборка. Тут я снова вспомнил про пример о трёх книжках с полки. Ага, значит нужно результат разделить на 2!.Так, так, так, следующая пара это уже 8 и 7 способов, во,во,во, истина где-то рядом. Так получается, что в числителе начинает вырисовываться факториал. $\frac {10\cdot9}{2!} \cdot \frac {8\cdot7}{2!} \cdot \frac {6\cdot5}{2!} \cdot \frac {4\cdot3}{2!} \cdot \frac {2\cdot1}{2!} = \frac{10!}{2!\cdot2!\cdot2!\cdot2!\cdot2!}$
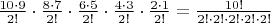
Начинает вырисовываться очень интересная картинка:
1. Во-первых очень знакомая получается дробь, это ничто иначе как перестановки с повторениями. Как они тут появилась я так и не понял, ведь в задаче нет повторений и люди, и пары, и даже стулья все разные. Ну если только то, что они все с одного завода , хоть и из разных филиалов .
2. Во-вторых в знаменателе нарисовалась та самая двойка $2^5$.

В результате получилась формула для подобного вида задач: $S=\frac{(n \cdot m)!}{(m!)^n}$
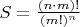
где n - количество филиалов, m - количество представителей из одного филиала

[mihaild]

ukatan в сообщении #1695296 писал(а):

ведь в задаче нет повторений и люди, и пары, и даже стулья все разные

Если подгонять под ответ - то, видимо, считается, что из люди из одного филиала одинаковые. Но формулировка задачи так себе, конечно.

[ukatan]

mihaild в сообщении #1695299 писал(а):

Но формулировка задачи так себе, конечно.

Да не вопрос.

Задача №1 версия 2
Есть клеммная колодка


И пять перемычек


Сколько существует способов установить все перемычки?