Я изучаю кратное отображение Абеля-Якоби по книге Гриффитса, Харриса Принципы алгебраической геометрии. Мне не совсем понятны их вычисления матрицы Якоби этого отображения в одном частном случае. Например на с. 368-369 они пишут:
Цитата:
Напомним некоторые обозначения:

- базис пространства голоморфных 1-форм на римановой поверхности

рода

отображение
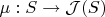
задается формулой
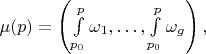
а отображение
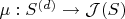
- формулой
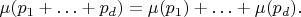
Если мы фиксировали локальную карту

на
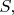
можно определить функции
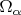
соотношениями
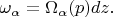
Очевидно, что вектор
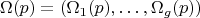
представляет точку

на канонической кривой из
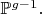
Я опущу их вычисления матрицы Якоби в случае, когда дивизора
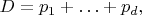
где все

различны. Далее они пишут.
Цитата:
Покажем теперь, что происходит на диагонали
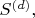
на примере дивизора
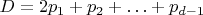
с различными точками
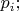
рассмотрение более общего случая отличается лишь более громоздкими обозначениями. Пусть

- координата точки

меняющейся в окрестности точки

а
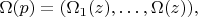
как и выше. Положим
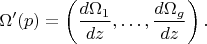
Тогда прямая
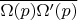
из
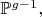
определяемая векторами
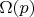
и
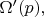
совпадает с касательной прямой к канонической кривой в точке

Для
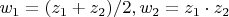
положим
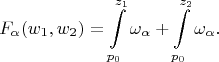
Но
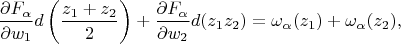
откуда
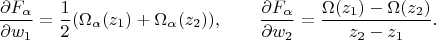
Устремляя

к

(координате точки

), мы получаем, что матрица Якоби отображения

в точке
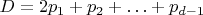
равна
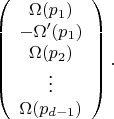
Я попыталась повторить последние вычисления. В результате у меня получилось то же выражение для частной производной
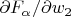
(не понятно, куда потерялись индексы

в книге), а выражение для
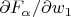
получилось совершенно другим. Не могу понять, где я ошиблась. Помогите разобраться, пожалуйста.