Максимальный идеал, не содержащий мультипликативную систему

[Naf2000]

Задача: Пусть в коммутативном кольце A с единицей задана мультипликативная система (содержит 1, не содержит 0) S. Пусть I - максимальный идеал, среди тех, которые не пересекаются с S. Доказать, что I - простой идеал в A.

Мое решение: Рассмотрим локализацию исходного кольца по S и рассмотрим гомоморфизм $\varphi(a)=a/1$
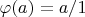
В таком случае образ идеала I порождает идеал $J=\left\langle\varphi(I)\right\rangle$=$\left\lbrace u/s: u \in I, s \in S \right\rbrace$
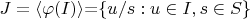
Идеал J - собственный, т.к. не содержит 1 кольца (следует из того, что $I \cap S = \varnothing$)
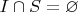
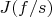
Пусть $ J(f/s)$ - расширение идеала элементом $f/s, f \notin I, s \in S$.
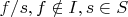
Очевидно, это расширение совпадает с расширением $ J(f/1)$.
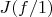
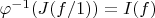
Прообразом этого расширения будет $\varphi^{-1}(J(f/1))=I(f)$, но согласно максимальности I следует $\exists s \in S\cap I(f)$.
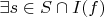
Значит $\varphi(s)=s/1 \in J(f) \Rightarrow 1 \in J(f) \Rightarrow J(f)=A$
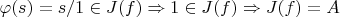
J - максимальный идеал в локализации A по S, а значит является простым.
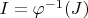
Прообраз простого идеала $I=\varphi^{-1}(J)$ является простым идеалом.

Все ли верно в рассуждениях? Можно ли обойтись в доказательстве без перехода к локализации?

[dgwuqtj]

Naf2000 в сообщении #1694769 писал(а):

Прообразом этого расширения будет $\varphi^{-1}(J(f/1))=I(f)$

Прообраз ещё будет содержать всякие элементы $x$, для которых найдётся $s \in S$ такое, что $x s \in I(f)$.

Naf2000 в сообщении #1694769 писал(а):

Можно ли обойтись в доказательстве без перехода к локализации?

Конечно, можно, притом прямо по определению.

[Naf2000]

Вторая попытка.
Пусть I - не является простым. Тогда найдутся $x_1, x_2 \in A \setminus I \Rightarrow {x_1}{x_2} \in I$.
Рассмотрим расширение идеала $I(x_1)$. В нем найдется $s_1=u_1+{a_1}{x_1}, s_1 \in S, u_1 \in I, a_1 \in A$.
Аналогично для второго элемента: $s_2=u_2+{a_2}{x_2}, s_2 \in S, u_2 \in I, a_2 \in A$.
Перемножая, получаем: ${s_1}{s_2} \in I$, что противоречит замкнутости S по умножению.
Следовательно I - простой идеал.

[dgwuqtj]

Теперь всё верно.