Век. Киллинга в пр. конст. кривизны Maple

[UmnyjDurak]

В одной статье автор вроде как нашел векторы Киллинга для пространств постоянной кривизны. В локальных координатах, в которых метрический тензор имеет вид:
$ g = \frac{dq^1 \otimes dq^1 + \dots + dq^m \otimes dq^m}{[1 + \frac{K}{4}((q^1)^2 + \dots + (q^m)^2)]^2}$,
где $K$ константа, векторы Киллинга по этой статье выглядят так:

$\tilde{R}_{ij}&= q^j \frac{\partial}{\partial q^i} - q^i \frac{\partial}{\partial q^j} \quad (1 \leqslant i < j \leqslant m),\\ \tilde{T}_i &= \left(2(q^i)^2 + \frac{K}{4} - \sum_{j=1}^{m} (q^j)^2\right) \frac{\partial }{\partial q^i} + 2\sum_{j=1}^{m} q^jq^i\frac{\partial}{\partial q^j} \quad (1 \leqslant i \leqslant m)$.

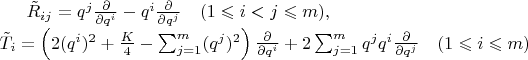
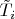
Вот только эти $ \tilde{T}_i$ векторами Киллинга не являются (если подставить и проверить). В статье достаточно много опечаток,
возможно тут просто где-то автор забыл приписать какой-то множитель. Я поэтому хотел бы попросить кого-нибудь, кто умеет работать с Maple, попробовать вбить ему эту метрику например для 2D случая, может он сможет векторы Киллинга найти а я уже потом из этого возможно исправлю для н-мерного пространства.

(В Maple вроде есть команда "найти век. Киллинга для заданной метрики", я сомневаюсь, что у него получится, но кто знает. Возможно такое есть и в Mathematica Вольфрама, но про это не слышал. К слову, не умею пользоваться ни одним из них, поэтому собственно и просьба.)

[UmnyjDurak]

Я таки достучался до остатков своего интеллекта и вроде как нашел эти векторы вручную (может быть даже правильно). Собственно, для тех, кто провел много бессонных ночей в переживаниях по поводу судьбы этого вопроса:
$\tilde{T}_i &= \left(4 - K\sum_{j=1}^{m} (q^j)^2\right) \frac{\partial }{\partial q^i} + 2K\sum_{j=1}^{m} q^jq^i\frac{\partial}{\partial q^j} \quad (1 \leqslant i \leqslant m)$.