Геометрия, вступительная задача в 10 класс (школа 57)

[Pripyat]

Добрый день. Встретил задачу в варианте вступительного экзамена в 10 класс:

Цитата:

Дано $DA'+DC'=DB'$. Докажите, что $ABCD$ вписанный.

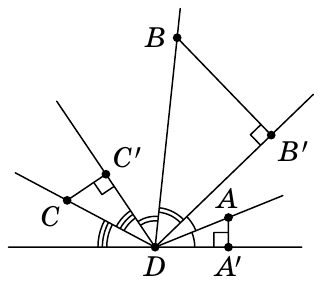
Честно говоря, долго искал решение, нашёл и не очень красивое. Поэтому, прошу подсказать более красивый способ решения.

Мой способ решения:

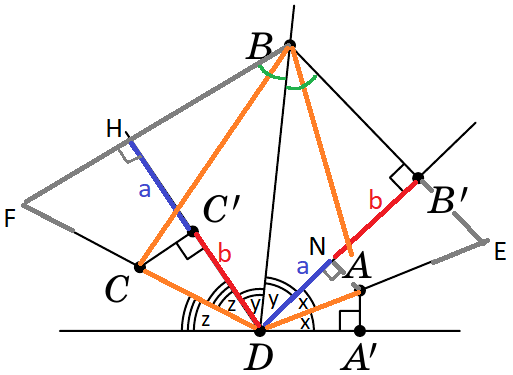
1. Обозначим углы, как показано на рисунке, тогда очевидно, что $x+y+z=90^\circ$.
2. Точка B равноудалена от сторон угла, значит видно равенство треугольников $\triangle DBH=\triangle DBB'$ и равенство углов $\angle FBD=\angle DBE$. Причём, так как треугольники прямоугольные, то $\angle FBD=\angle DBE = 90^\circ-y = x+z$.
3. По условию $DA'+DC'=DB'$, также $DA' = DN = a$. Тогда $AB' = DC' = b$ и $C'H = DN = a$.
4. Угол $\angle DFB = 90^\circ-z = x+y$ (из прямоугольного треугольника $\triangle FDH$), угол $\angle DEB' = 90^\circ-x = y+z$ (из прямоугольного треугольника DB'E).
5. Рассмотрим треугольники $\triangle FBD=\triangle DBE$. Они подобны, так как углы равны. Тогда $\frac{FB}{BD} = \frac{FD}{DE} = k$
6. Также видно, что подобны треугольники $\triangle FBC=\triangle DBA$ по углу и двум пропорциональным сторонам.
Действительно, углы $\angle BFD=\angle BDE$, $\frac{FB}{BD} = k$ и $\frac{FC}{DA} = \frac{a}{a+b}FD :\frac{a}{a+b}DE= \frac{FD}{DE} = k$.
7. Тогда углы $\angle FBC=\angle DBA$, значит можно найти угол $\angle ABC = \angle FBD-\angle FBC +\angle DBA = \angle FBD = x+z$
8. Наконец, в четырехугольнике ABCD: $\angle B+\angle D = (z+y+y+x) + (x+z) = 2(x+y+z) = 180^\circ$. Значит, он вписанный (ч.т.д.)

[TOTAL]

Условие полностью приведите.

[Pripyat]

Условие дано именно в таком виде (приложена вырезка из непосредственно варианта):

[TOTAL]

Вот простое решение.

Жирные точки лежат на одной окружности.

[Pripyat]

TOTAL, спасибо. Да, это действительно так.
Однако остаются вопросы:
1) Как привести конфигурацию исходной задачи к Вашей
2) Есть важное условие $DA'+DC'=DB'$, без выполнения которого четырехугольник необязательно вписанный. Не очень понятно, как оно использовалось в решении.

[TOTAL]

Pripyat в сообщении #1691979 писал(а):

1) Как привести конфигурацию исходной задачи к Вашей

Моя превращается в исходную, если разрезать фигуру по диагонали прямоугольника, затемо правую часть перевернуть на левую сторону и пристыковать на прежнее место.