Об осевом моменте инерции сечения

[yatupoinebeite]

Здравствуйте. Решил ради самообразования научиться находить момент инерции произвольного сечения.
Что я знаю об этом моменте?
Осевой момент инерции сечения относительно выбранной оси - это величина, характеризующая распределение площади сечения относительно данной оси и определяющая его сопротивление изгибу.
Вычисляется он так:
I_x = $$\int\limits_{A}^{}$$y^2dA,
где I_x – собственно осевой момент инерции сечения относительно оси x, измеряется в единицах длины в четвёртой степени, например {см}^4;
A – площадь сечения;
y^2 – квадрат расстояния от элементарной площадки площадью A сечения до оси x;
dA – площадь произвольной бесконечно малой площадки в сечении.

Для оси y этот момент вычисляется по формуле
I_y = $$\int\limits_{A}^{}$$x^2dA,
где I_y – осевой момент инерции сечения относительно оси y;
x^2 – квадрат расстояния от элементарной площадки площадью A сечения до оси y.

Выглядит формула прекрасно, только вот я, к сожалению, не понимаю, как её применить.

На одном из сайтов приведена такая картинка:

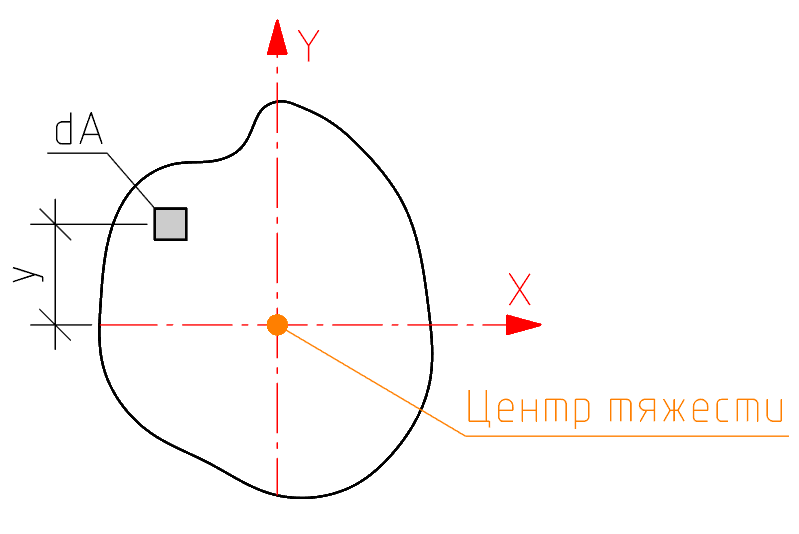
Красиво, но я не пойму, отчего элементарная площадка взята именно в том месте вдоль оси x, где она взята, а не в каком-нибудь другом месте, и как согласно этой схеме всё-таки вычислить момент инерции.

Но та картинка иллюстрирует принцип, а вот реальная задача.
Итак, дано поперечное сечение уголка 30х30х3 по ГОСТ 8509-93. Вот так оно выглядит:

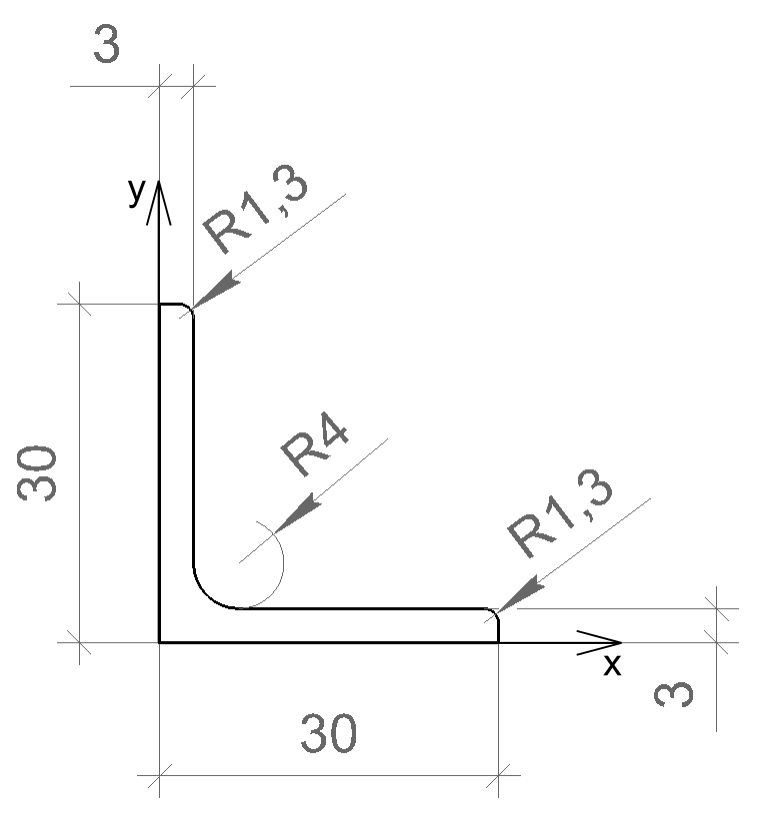
Площадь поперечного сечения – 173.71 {мм}^2, что равно 1,73 {см}^2.
ГОСТ 8509-93 даже дает справочное значение момента инерции (правда, центробежного, а не осевых):
I_{xy} = 0.89 {см}^4.

Кажется, для вычисления момента инерции есть все. Вычисляем:
I_x = $$\int\limits_{A}^{}$$y^2dA;
Поскольку y не является функцией площади
y $\ne$ f(A),
при раскрытии интеграла y я принимаю как константу.
I_x = A $\cdot$ y^2 + C.
Подставляем в выражение значение площади сечения, известное заранее:
I_x = 1.73 $\cdot$ y^2 + C,

и получается каша. Ошибка есть, это очевидно, но правильного пути я пока не вижу.
Есть пробел, пробел огромный, и я не понимаю, как его закрыть.
Прошу вашего совета: в каком направлении думать, чтобы решить эту задачу?
Заранее спасибо.

[Утундрий]

yatupoinebeite в сообщении #1691377 писал(а):

Выглядит формула прекрасно, только вот я, к сожалению, не понимаю, как её применить.

Для этого нужно сперва свести поверхностный интеграл к повторному.

[sergey zhukov]

yatupoinebeite
Интеграл по площади - это двойной интеграл. Должна быть функция двух переменных (от $x$ и $y$). От нее сначала берется интеграл по $y$ (в пределах, которые являются функцией $x$), и получается только функция от $x$. А потом от нее нужно взять интеграл по $x$.

Можете попроще задачу решить. Например, найти методом интегрирования площадь круга. Там совершенно тот же прием используется.

Можно это так представлять, что сначала тело разбивается на тонкие элементарные полосы (скажем, параллельные $y$) толщиной $dx$, и наша первая задача - найти площадь полосы, как функцию $x$ (это первое "вертикальное" интегрирование вдоль $y$ - вычисление площади элементарной полосы). А потом нужно сложить площади всех элементарных полос (второе "горизонтальное" интегрирование вдоль $x$).

Поиск момента инерции отличается только тем, что площадь каждой элементарной полосы нужно еще умножить на квадрат расстояния от нее до выбранной оси (если за ось выбрана ось $y$, то это значит, что нужно умножать на $x^2$).

Например, площадь четвертушки круга радиуса $R$ вычисляется так:

$$S=\int\limits_{0}^{R}(\int\limits_{0}^{\sqrt{R^2-x^2}}dy)dx$$

А ее момент инерции относительно, например, оси $y$:

$$S=\int\limits_{0}^{R}(x^2\int\limits_{0}^{\sqrt{R^2-x^2}}dy)dx$$

В выражении для площади внутренний интеграл, умноженный на $dx$ - площадь вертикальной элементарной полосы шириной $dx$ (на которые разбита четвертушка круга) находящейся на расстоянии $x$ от оси $y$. Это функция $x$. Наружный интеграл складывает все эти полосы в пределах четвертушки круга.

Последний интеграл можно и так записать:

$$S=\int\limits_{0}^{R}\int\limits_{0}^{\sqrt{R^2-x^2}}x^2dxdy$$

Здесь $dxdy$ - это и есть $dA$.

[Утундрий]

sergey zhukov в сообщении #1691419 писал(а):

$$S=\int\limits_{0}^{R}(\int\limits_{0}^{\sqrt{R^2-x^2}}dy)dx$$

Нотация "дифференциал сразу после знака интеграла" в данном случае будет выглядеть более эстетично.

[yatupoinebeite]

sergey zhukov
Я очень вам благодарен за подробный ответ. Сейчас ваше пояснение для меня – самый ценный источник информации по вопросу.

[Утундрий]

yatupoinebeite
И какое это имеет значение? Фантиками в виде лайков здесь не балуются.

[EUgeneUS]

Утундрий в сообщении #1691387 писал(а):

я этого нужно сперва свести поверхностный интеграл к повторному.

ИМХО, нужно понять, что же собственно считается.
А сведение поверхностного интеграла к повторному - это метод вычисления.

-- 20.06.2025, 19:27 --

yatupoinebeite в сообщении #1691377 писал(а):

Выглядит формула прекрасно, только вот я, к сожалению, не понимаю, как её применить.

yatupoinebeite в сообщении #1691377 писал(а):

Красиво, но я не пойму, отчего элементарная площадка взята именно в том месте вдоль оси x, где она взята, а не в каком-нибудь другом месте, и как согласно этой схеме всё-таки вычислить момент инерции.

Вы понимаете, что интеграл (любой определенный) - это предел интегральных сумм?
Если бы понимали, то было бы ясно, что "элементарная площадка взята" не в каком-то конкретном месте "вдоль оси $x$". А на рисунке указана одна из множества площадок, которые заполняют всё сечение.

А интеграл по поверхности - это предел суммы по этим площадкам, если площадь каждой площадки стремится к нулю (а количество площадок, конечно, к бесконечности).

То есть процедура такая:
1. Разбиваем поверхность на $N$ площадок ($N$ пока конечное).
2. Умножаем площадь каждой площадки на что-нибудь, в зависимости от того, какую величину считаем.
3. Это интегральная сумма.
4. Потом разбиваем поверхность на всё более мелкие площадки (и делаем тоже самое, что в пп. 1-2), и устремляем количество площадок к бесконечности. Этот предел и будет поверхностным интегралом (поверхностным интегралом первого рода).

А уже потом методами матана доказывается, что его можно свести к повторному интегралу (в определенных случаях).

[Утундрий]

EUgeneUS в сообщении #1691529 писал(а):

ИМХО, нужно понять, что же собственно считается.
А сведение поверхностного интеграла к повторному - это метод вычисления.

Да тут хотя бы с методом разобраться. Своим первым комментарием я отметил место, с которого в рассуждениях ТС начинается дичь.