Односторонние обратные отображения

[Xo4y3HaTb]

Пусть $X=\lbrace x_1\rbrace, Y=\lbrace y_1, y_2\rbrace f: X\to Y (x_1\to y_1), g: Y\to X$. Пусть $Y'= \lbrace y_1, y_2, y_3\rbrace,$. Можно ли считать отображения $f:X\to Y$ и $f: X\to Y' (x_1\to y_1)$ равными, если я меняю только область прибытия функции? Если считать такие ф-и равными, тогда можно предоставить сколько угодно отображений $g$ - которые являются левыми обратными для $f$. Просто добавлять новый эл-т в мн-во $Y$ и отображать его в $x_1$. Но вот построить второе правое обратное отображение f для данного $g$ не выходит. Чтоб построить дополнительное отображение $f$ я должен увеличить мн-во $X$(или изменить $x_1$ на $x_2$, но тогда сразу изменится исходное отображение $g$). Добавлю $x_2$ в $X$, значит добавляется $y$ в $Y$,но чтобы выполнялось условие $g\circ f= e_x$ я должен сделать отображение g из $y$ в $x_2$, что уже нарушает равенство с исходным $g$. Т.е. построение многих правых обратных невозможно. Где ошибка в рассуждениях?

[mihaild]

Xo4y3HaTb в сообщении #1689675 писал(а):

Можно ли считать отображения $f:X\to Y$ и $f: X\to Y' (x_1\to y_1)$ равными, если я меняю только область прибытия функции?

В варианте Зорича - можно, т.к. функция - это просто множество пар, а множество пар одно и то же. Любая функция $X \to Y$ является по нему одновременно и функцией $X \to Y \cup Y'$ для любого $Y'$.
Есть альтернативное формальное определение функции, когда функция это тройка (домен, кодомен, функциональное отношение); по нему функции с разным кодоменом уже разные, но по нему нельзя брать композицию функции $X \to Y$ с функцией $Y' \to Z$ если $Y \neq Y'$. ИМХО гораздо интереснее подобрать пример, когда есть две разных обратных функции, определенных на одном и том же множестве.

[dgwuqtj]

Xo4y3HaTb в сообщении #1689675 писал(а):

Но вот построить второе правое обратное отображение f для данного $g$ не выходит.

Как это не выходит? Есть ровно два отображения $X \to Y$, одно из них — это ваше $f$, и второе тоже будет правым обратным к $g$.

[Xo4y3HaTb]

mihaild в сообщении #1689684 писал(а):

В варианте Зорича - можно, т.к. функция - это просто множество пар, а множество пар одно и то же. Любая функция $X \to Y$ является по нему одновременно и функцией $X \to Y \cup Y'$ для любого $Y'$.
Есть альтернативное формальное определение функции, когда функция это тройка (домен, кодомен, функциональное отношение); по нему функции с разным кодоменом уже разные, но по нему нельзя брать композицию функции $X \to Y$ с функцией $Y' \to Z$ если $Y \neq Y'$. ИМХО гораздо интереснее подобрать пример, когда есть две разных обратных функции, определенных на одном и том же множестве.

Является ли в таком случае кодомен областью значения функции, а не областью прибытия? Не выглядит ли условие $Y=Y'$ слишком строгим?) Ведь по сути, чтоб выполнялась композиция достаточно $Y\subset Y'$. В примере, когда есть две разных обратных функции определённых на одном и том же мн-ве условия $f: X\to Y, g: Y\to X, g\circ f=e_x$ сохраняются? Является ли в этом примере $Y$ кодоменом $f$ ($X$ кодоменом $g$)?

dgwuqtj в сообщении #1689685 писал(а):

Как это не выходит? Есть ровно два отображения $X \to Y$, одно из них — это ваше $f$, и второе тоже будет правым обратным к $g$.

Ой, точно! Просто отобразить $x_1\to y_2$. Получается левых отображений сколь угодно много, а правых не больше чем элементов мн-ва $Y$. Cпасибо!

[dgwuqtj]

Частично определённых отображений $Y \to \{x_1\}$ не сколь угодно много, а $2^{|Y|}$ штук (хотя и больше, чем $|Y|$).

[mihaild]

Xo4y3HaTb в сообщении #1689699 писал(а):

Является ли в таком случае кодомен областью значения функции, а не областью прибытия?

Ни то и не другое. Функция не обязана принимать все значения из кодомена, но кодомен в этом определении прибит к функции, и не любая область прибытия является кодоменом.

Xo4y3HaTb в сообщении #1689699 писал(а):

В примере, когда есть две разных обратных функции определённых на одном и том же мн-ве условия $f: X\to Y, g: Y\to X, g\circ f=e_x$ сохраняются?

Не очень понимаю вопроса. Да, определение левой и правой обратных функций сохраняются, и левые и правые обратные остаются неединственными.

[Xo4y3HaTb]

dgwuqtj в сообщении #1689706 писал(а):

Частично определённых отображений $Y \to \{x_1\}$ не сколь угодно много, а $2^{|Y|}$ штук (хотя и больше, чем $|Y|$).

. Да согласен, если частично определённое отображение это функция которая не обязана отображать каждый эл-т из области определения. Я имел ввиду именно левые обратные отображения. Они у меня не привязаны к мн-ву $Y$, я меняю $Y$ как хочу (не трогая $y_1\to x_1$), тогда $f$ остаётся неизменным и сохраняется выполнение условия $g\circ f=e_x$. Поэтому отображений $g$ - левых обратных сколь угодно много.

mihaild в сообщении #1689684 писал(а):

интереснее подобрать пример, когда есть две разных обратных функции, определенных на одном и том же множестве.

Пусть $X=\lbrace x_1, x_2\rbrace,Y=\lbrace y_1, y_2, y_3\rbrace f: x_1\to y_1, x_2\to y_2$, $ g: y_1\to x_1, y_2\to x_2, y_3\to x_1$.Если поменяю в $g: y_3\to x_2$, получу ещё одно левое обратное, при этом области не изменятся. В $f$ нужно отобразить $x_1\to y_3$.

Помогите, пожалуйста, понять пример с последовательностями, который предлагают рассмотреть. Что такое $a$ и $f_a$ в задаче? Судя по записи $(a, x_1,..,x_n,..)$ хочется сказать, что $a$ это эл-т какой-либо последовательности из $X$. Но тогда $f_a\neq f(a)$ т.к. в таком случае $a$ являлась бы последовательностью. Если же считать $a$ последовательностью, тогда не ясна запись $(a, x_1,..,x_n,..)$. Ещё думал над вариантом, что $f_a$ есть отображение всех посл-й содержащих элемент $a$, но такое отображение тоже не получилось построить, т.к. получаются только отношения. В общем опять путаница конкретная.

[mihaild]

Xo4y3HaTb в сообщении #1689829 писал(а):

Что такое $a$ и $f_a$ в задаче? Судя по записи $(a, x_1,..,x_n,..)$ хочется сказать, что $a$ это эл-т какой-либо последовательности из $X$.

$a$ - произвольное число. Для каждого числа рассматривается функция $f_a$.

Xo4y3HaTb в сообщении #1689829 писал(а):

Но тогда $f_a\neq f(a)$

Так а где написано что-то про $f(a)$?

[tolstopuz]

mihaild в сообщении #1689684 писал(а):

В варианте Зорича - можно, т.к. функция - это просто множество пар

Вообще-то нет, в неформальном определении Зорича функция - это тройка, а в теоретико-множественном "функция" - это просто множество пар, но есть еще "функция из $X$ в $Y$", которая требует для своего определения два множества и потому фактически тоже является тройкой.

-- Вт июн 10, 2025 19:21:31 --

mihaild в сообщении #1689684 писал(а):

но по нему нельзя брать композицию функции $X \to Y$ с функцией $Y' \to Z$ если $Y \neq Y'$.

У Зорича тоже нельзя.

mihaild в сообщении #1689709 писал(а):

не любая область прибытия является кодоменом.

Можете рассказать подробнее?

[mihaild]

tolstopuz в сообщении #1689844 писал(а):

но есть еще "функция из $X$ в $Y$", которая требует для своего определения два множества и потому фактически тоже является тройкой

Цитата:

Такое функциональное отношение $\mathcal R \subset X \times Y$ и есть отображение из $X$ в $Y$, или функция из $X$ в $Y$

tolstopuz в сообщении #1689844 писал(а):

У Зорича тоже нельзя.

Определение композиции отношений у него в 1м упражнении. Где там такие ограничения?

tolstopuz в сообщении #1689844 писал(а):

Можете рассказать подробнее?

Вот ровно над первым Вашим скриншотом написано определение

Цитата:

любое множество $Y$, содержащее область значений функции, называют тогда областью ее прибытия

[Xo4y3HaTb]

tolstopuz в сообщении #1689844 писал(а):

Вообще-то нет, в неформальном определении Зорича функция - это тройка, а в теоретико-множественном "функция" - это просто множество пар, но есть еще "функция из $X$ в $Y$", которая требует для своего определения два множества и потому фактически тоже является тройкой.

Я тоже сначала подумал, о функции как о тройке. В задаче 6 из Зорича говорится, что для ЛЮБЫХ отображений вида $f: X\to Y, g: Y\to X, g\circ f=e_x$ существует много односторонних левых и правых обратных. Если будем считать, что функции разные при разных областях прибытия, то в приведённом изначально примере получаем противоречие с условием. $X=\lbrace x_1\rbrace, Y=\lbrace y_1, y_2\rbrace f: X\to Y (x_1\to y_1), g: Y\to X$. Невозможно представить второе отображение $g$ не изменяя область $Y$.

Про кодомен тоже интересно, т.к. в статье Вики картинка показывает, что кодомен = область прибытия



Кстати, тут мне не до конца ясно. Судя по математической записи области $Y$ должны совпадать, но словами говорится, если $g$ определено на мн-ве значений $f$.... Т.е. любое отображение область определения которого содержит мн-во значений $f$ определено на мн-ве значений $f$, а потому оно подходит под определение.

mihaild в сообщении #1689830 писал(а):

$a$ - произвольное число. Для каждого числа рассматривается функция $f_a$.

Разобрался, спасибо!

[tolstopuz]

mihaild в сообщении #1689848 писал(а):

Определение композиции отношений у него в 1м упражнении. Где там такие ограничения?

Отношений - да, но не функций (см. скриншот). Немного не к месту здесь выглядит упоминание области значений, но, как ни странно, по сути это верно (хотя и ни к чему здесь) - $g$ может быть даже частично определенной функцией на $Y$, лишь бы ее домен содержал область значений $f$.

mihaild в сообщении #1689848 писал(а):

Вот ровно над первым Вашим скриншотом написано определение

Цитата:

любое множество $Y$, содержащее область значений функции, называют тогда областью ее прибытия

Да, тут у него действительно немного мутно. В основном из-за того, что "функция" и "функция из $X$ в $Y$" - разные понятия. У него тут такая последовательность:
1) берем произвольную функцию $f$;
2) вычисляем ее область определения $X$ и область значений $Y$;
3) берем произвольное множество $Y'\supset Y$;
4) получившуюся тройку $(X,f,Y')$ называем функцией из $X$ в $Y'$.

У тройки, получившейся в пункте $4$, одна вполне определенная область прибытия, она же кодомен, и в упражнении идет речь именно о функциях-тройках. А просто нетипизированные функции без указания домена и кодомена, кажется, у Зорича далее определения вообще не встречаются.

Подход немного старомодный, но вполне рабочий, у Куратовского-Мостовского точно так же. У Келли вообще тройки не строятся, а вводится двуместный предикат "$f$ - отображение в $Y$" (а для сюръективности - "$f$ - отображение на $Y$").

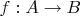
У Манкрза еще смешнее - он честно определяет $r\subset C\times D$, требует его инъективность, потом обозначает $A=\operatorname{pr}_1 r$, выбирает $B$, чтобы $\operatorname{pr}_2 r\subset B\subset D$, и выкидывает $C$ и $D$ за ненадобностью, оставляя пару $f=(r,B)$, обозначаемую $f: A\to B$.

[mihaild]

Xo4y3HaTb в сообщении #1689849 писал(а):

кодомен = область прибытия

Нет. Кодомен единственный, а областей прибытия много.

Xo4y3HaTb в сообщении #1689849 писал(а):

Судя по математической записи области $Y$ должны совпадать, но словами говорится, если $g$ определено на мн-ве значений $f$

Отображение $X \to Y$ по Зоричу одновременно является и отображением $X \to Y \cup Y'$. Хотя сформулировано всё равно несколько мутно, да.

tolstopuz в сообщении #1689892 писал(а):

получившуюся тройку $(X,f,Y')$ называем функцией из $X$ в $Y'$

Вот я не вижу, где у него это написано.

Впрочем, это всё не очень важно. ИМХО изначальное упражнение - на понимание, что левое обратное может как угодно себя вести вне образа исходной функции, а правое - отправлять элемент в любой из его прообразов относительно исходного.

[tolstopuz]

mihaild в сообщении #1689895 писал(а):

Отображение $X \to Y$ по Зоричу одновременно является и отображением $X \to Y \cup Y'$.

Что же такое сюръекция? :)

mihaild в сообщении #1689895 писал(а):

Вот я не вижу, где у него это написано.

Именно поэтому по Зоричу не стоит самостоятельно учить основы теории множеств :)

На стр. 15 он определяет функцию как тройку, на стр. 25 забывает об этом и определяет как функциональное отношение, через шесть строк вспоминает, но формулирует до такой степени по-другому, что некоторые понимают его и противоположным образом. На стр. 26 возвращается к стр. 15 в выражении "функции, понимаемой в смысле исходного описания".