Опрос: Где лето жарче?

[Mihr]

Ещё один опрос. Просьба всё та же: отвечать по памяти, никуда не подглядывая.

Известно, что орбита Земли имеет небольшой эксцентриситет. Благодаря ему жители Северного полушария оказываются зимой чуть ближе к Солнцу, чем летом. Поэтому, возможно, лето в Северном и Южном полушариях несколько разное. Что Вы думаете (или просто помните) по этому поводу?

[Gagarin1968]

Думаю, что лето в Южном полушарии всё же холоднее, чем в Северном. Ведь в Южном полушарии океаны занимают около 80% от общей площади земной поверхности. А вода, как известно, медленнее, чем суша, нагревается и медленнее остывает. Но за 3 летних месяца (с декабря по март) такая огромная масса воды просто не успевает нагреться. И всё это влияет на летнюю температуру. В Северном полушарии она повыше.

[sergey zhukov]

Mihr
Думаю, это как с влиянием вращения Земли на направление закручивания водяной воронки в разных полушариях: оно есть, но другие факторы гораздо сильнее. Т.е. лето наверняка различается, но в первую очередь не по этому.

Основные факторы, как мне кажется: разница в распределении воды и суши, разница в воздушных и океанических течениях. На совершенно однородной гладкой Земле уже эксцентриситет будет иметь значение.

[Mihr]

sergey zhukov, я сам не пытался что-то здесь просчитывать, так что никаких оценок Вашим рассуждениям давать не буду. Скажу пока лишь одно: я встречал другое объяснение, и связано оно было именно с эксцентриситетом орбиты Земли.

[Booker48]

Mihr в сообщении #1686737 писал(а):

чуть ближе к Солнцу

Это "чуть" - 5 млн км, больше 3%.

[EUgeneUS]

Указал второй вариант. Но из тех же соображений, что и Gagarin1968

[Mihr]

Booker48 в сообщении #1686789 писал(а):

Это "чуть" - 5 млн км, больше 3%.

Это, по-Вашему, много?

[worm2]

Mihr в сообщении #1686801 писал(а):

Это, по-Вашему, много?

Расстояние, меньшее на 3% — это на 6% больший поток тепла.
Дальше мысль останавливается, но если подходить к вопросу чисто нумерологически, 6% от типичной температуры поверхности Земли в Кельвинах — это величина порядка десяти градусов.

[Ghost_of_past]

Более жаркое в Северном полушарии - и насколько я помню из школьной географии, основная причина тут всё-таки, и правда, в соотношении площадей суши и океана, которые прогреваются с разной скоростью.

[Mihr]

Ghost_of_past в сообщении #1686848 писал(а):

и насколько я помню из школьной географии, основная причина тут всё-таки, и правда, в соотношении площадей суши и океана, которые прогреваются с разной скоростью.

Возможно, это и есть основная причина, не спорю. Но я встречал иное объяснение. В окрестности афелия планета движется медленнее, чем в окрестности перигелия. Поэтому "летнее полугодие" для Северного полушария несколько продолжительнее "зимнего". И так как лето в Северном полушарии де-факто продолжительнее, чем в Южном, то и успевает Земля прогреться Северным полушарием более основательно, чем Южным.

[Ghost_of_past]

Mihr в сообщении #1686858 писал(а):

Но я встречал иное объяснение. В окрестности афелия планета движется медленнее, чем в окрестности перигелия. Поэтому "летнее полугодие" для Северного полушария несколько продолжительнее "зимнего".

Вполне вероятно, что в какой-то доли влияет и то, и другое.

[sergey zhukov]

Mihr
Эффект от эксцентриситета орбиты работает против эффекта от неравномерной скорости на орбите. Если бы они еще складывались.

[Anton_Peplov]

На климат Южного полушария большое влияние оказывает и Антарктида. Она источник холодных течений и ветров. Из-за них, например, на Фолклендских островах в самый теплый сезон +9 по Цельсию, хотя они ближе к экватору, чем Москва.

[sergey zhukov]

Всегда хотел посчитать модельную задачу распределения среднегодичного освещения поверхности шара, который имеет орбитальное, собственное вращение и наклон оси к плоскости орбиты (круговой).
Если орбитальное и собственное вращения не кратны (и собственное вращение заметно быстрее орбитального), то распределение среднегодичной освещенности зависит только от широты и получается вот что (за единицу освещенности принимается постоянно падающий нормальный поток, расчет для нескольких углов наклона оси вращения):

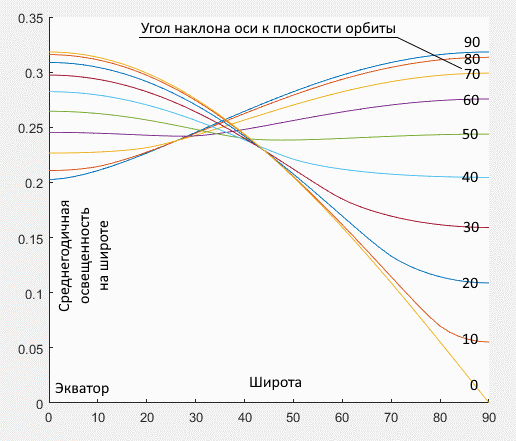
В любом случае любая точка поверхности получает не более трети максимально возможного освещения. Где-то в районе наклона $50^{\circ}$ среднегодичное распределение по всей поверхности наиболее равномерное.
Если же частоты орбитального и собственного вращения не кратны, то распределение освещенности зависит как от широты, так и от долготы. Некоторые примеры (показано соотношение частот орбитального/собственного вращения и угол наклона оси вращения к плоскости орбиты, ориентация, как у стандартной географической карты (полюса вверху и внизу, долгота по горизонтали)):

Появляются горячие и холодные пятна, в которых иногда достигается максимально возможная и нулевая освещенность. Имеет значение, противоположно собственное вращение орбитальному или нет.

Можно и эксцентриситет сюда добавить.

[Serg53]

Mihr в сообщении #1686737 писал(а):

возможно, лето в Северном и Южном полушариях несколько разное. Что Вы думаете (или просто помните) по этому поводу?

Параметр "температура полушария планеты" слишком абстрактен. Не лучше ли сравнивать температуры конкретных точек планеты?
Остров Пасхи — Википедия -
https://ru.wikipedia.org/wiki/%D0%9E%D1 ... 1%85%D0%B8

Цитата:

Климат острова Пасхи тёплый, тропический.
Средняя годовая температура 21,8 °C, самый холодный месяц август (19,2 °C), самый тёплый - январь (24,6 °C).