Всем привет
Решаю такую задачу. Может быть она где-то уже решена
Пусть
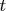
— случайная величина, распределённая по экспоненциальному закону с плотностью вероятности:

где

— известный параметр распределения.
Пусть число
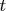
сгенерировано из этого распределения, однако его значение нам не известно. Вместо этого дана дополнительная информация: известно, что

,
где
![$ a \in [1, 29] $ $ a \in [1, 29] $](https://dxdy-03.korotkov.co.uk/f/2/8/1/2818548476dbeada17c063b3d468729a82.png)
.
Требуется найти условную вероятность того, что

, при условии, что

. То есть, найти аналитическое выражение для вероятности

То, до чего смог дойти
Так как экспоненциальное распределение обладает свойством отсутствия памяти, условная вероятность вычисляется как:
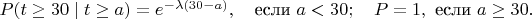
Но, сделал Монте-Карло и не очень совпадает. При

ну вроде неплохо совпадает, но при

не совпадает совсем
Подскажите куда двигаться в каком направлении