Уважаемые участники форума!
Я хочу поделиться дополненной версией моего подхода в рамках Теории Информационного Проецирования (ТИП) и прошу вас дать обратную связь. Ниже приведены основные положения с дополнениями, которые, на мой взгляд, являются ключевыми.
Постулаты
1. Абсолютное время:
• Время вводится как универсальный, неизменный параметр, который не подвергается искривлению
и остаётся одинаковым для всех наблюдателей.
• Все динамические процессы происходят исключительно в пространственных измерениях, а время
служит внешней "координатой эволюции" системы.
2. 4‑мерное чисто пространственное множество:
• Полное пространство описывается как 4‑мерное, то есть имеет четыре чисто пространственных измерения.
• Вместо стандартной схемы "3 плюс 1", где время смешивается с пространством, в нашей модели
все искривления и деформации происходят только в пространственных координатах.
• Это означает, что 4‑е пространство (четвертое чисто пространственное измерение) является полноценно
интегрированной частью геометрии, а не временной координатой.
3. Проекция в наблюдаемое пространство:
• Наблюдаемое 3‑мерное пространство получается в результате проекции полного 4‑мерного описания.
• При этом происходит усреднение или потеря части информации (вытекает квантовая неопределённость),
что объясняет появление эффектов, характерных для квантового мира.
4. Универсальность физических законов:
• Фундаментальные законы, записанные на уровне полного 4‑мерного пространственного описания
(с абсолютным временем), являются строго инвариантными и не зависят от системы отсчёта.
• Нарушения инвариантности наблюдаются лишь как побочный эффект проекции от 4‑мерного описания
в наблюдаемое 3‑мерное пространство, а не из-за природы физических процессов.
--------------------------------------------------
2. Преобразования Галилея с учётом сжатия
В классической механике преобразования Галилея записываются как:

Это отражает абсолютное время.
В ТИП полный 4‑мерный детерминированный процесс сохраняется, а наблюдаемое 3‑мерное пространство получается посредством оператора проекции. При этом поперечная компонента (катета) сжимается по Лоренцеву фактору:





--------------------------------------------------
3. Интервал в эллипсоидальном пространстве
В условиях эллипсоидального сжатия путь света из точки A в точку B и обратно состоит из двух отрезков

и

, причем их сумма постоянна:

где

– большая полуось эллипсоида.
Интервал для "туда-обратно" пути определяется как:
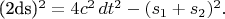
Подставляя

получаем:

Определив среднюю скорость света в эллипсоидальном пространстве как:

интервал примет вид:

--------------------------------------------------
4. Сложение скоростей в условиях эллипсоидального сжатия
Общая формула сложения скоростей в данной модели:

В упрощённом случае (при движении вдоль ортогональных осей, например,

и

):

Особое внимание хочется уделить тому, что сложение ортогональных скоростей в этой модели даёт именно средний путь, что вытекает из свойств эллипсоида. Геометрически, если вектор

задаёт сдвиг, а

– перемещение относительно него, то благодаря свойству эллипсоида (сумма расстояний от любой точки до двух фокусов постоянна) получаем:

--------------------------------------------------
5. Инвариантность 4‑мерного интервала и переход к проекции
Полная 4‑мерная инвариантность обеспечивается тем, что полный 4‑мерный интервал можно разложить на наблюдаемую 3‑мерную проекцию и ее дополнительную, скрытую составляющую:

Это означает, что независимо от угла проекции

полный интервал

сохраняется неизменным. В частности, если принять, что наблюдаемая 3‑мерная компонента равна:

а соотношение

задаёт эффект Лоренцевого сжатия, то сумма квадратичных проекций (наблюдаемой и скрытой) равна исходному 4‑мерному интервалу.
--------------------------------------------------
Заключение и просьба о комментариях:
Согласно ТИП, основное движение происходит в полном 4‑мерном пространстве, а наблюдаемая 3‑мерная картина является результатом проекции с потерей информации – это приводит к появлению эффектов, таких как квантовая неопределённость, а также наблюдаемым отклонениям (например, в сложении скоростей или измерении интервала).
Особое внимание хочу обратить на два аспекта:
1. Полная 4‑мерная инвариантность, выраженная формулой

доказывает, что независимо от угла проекции сохранён полный интервал.
2. Сложение ортогональных скоростей в этой модели описывается через средний путь, что следует из геометрических свойств эллипсоида, задающего, как именно складываются вкладные скорости.
Прошу вас прокомментировать:
- Насколько понятна идея полной 4‑мерной инвариантности через вышеуказанную формулу?
- Согласны ли вы с тем, что сложение ортогональных скоростей определяется через средний путь (как следует из свойств эллипсоида)?
- Почему, по вашему мнению, этот переход от 4‑мерного интервала к наблюдаемой 3‑мерной проекции является ключевым?
Буду благодарен за ваши отзывы и предложения по улучшению данной модели. Спасибо за внимание!