Функция распределения и плотность

[paranoidandroid]

Задача 1. Плотность случайной величины $\xi$ равна $ f_{\xi}(x)=\frac{1}{2 \pi} e^{- \frac{x^2}{2}} $. Найдите функцию распределения и плотность случайной величины $\eta={\xi}^5$.

Решение: Чтобы узнать плотность, из теории знаем, что $ f_{\eta}=f_{\xi}(g^{-1}(x))|(g^{-1}(x))'| $ ; $ \eta=g(\xi) $ ($g(x)$ строго монотонная функция).

В нашем случае:

$f_{\eta}(x)=\frac{1}{2 \pi} e^{- \frac{x^2/5}{2}}|(x^{1/5})'| \Rightarrow f_{\eta}(x)=\frac{1}{10 \pi} e^{- \frac{x^2/5}{2}} x^{-4/5}$.

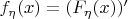
$f_{\eta}(x)=(F_{\eta}(x))'$ , Где $F_{\eta}(x)$ - функция распределения.

В нашем случае: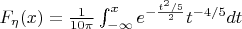

$F_{\eta}(x)=\frac{1}{10 \pi} \int_{- \infty}^{x}e^{- \frac{t^2/5}{2}} t^{-4/5}{dt}$.

Задача 2. Известно, что случайная величина $\xi$ имеет нормальное $N(0,1)$ распределение. Найдите функцию распределения и плотность случайной величины $\eta=3\xi+18$.

Решение:

Теория: $ F_{\eta}(x)=F_{\xi}(g^{-1}(x)) $ Где $ \eta = g(\xi) $ является строго возрастающей функцией.

В нашем случае:


Я думаю, здесь следует предположить, что $f_{\xi}(x)$ И $ F_{\xi} $ Известные функции и по формуле
$ f_{\eta}=f_{\xi}(g^{-1}(x))|(g^{-1}(x))'| $:

$f_{\eta}(x)=f_{\xi}(\frac{x-18}{3}) \cdot \frac{1}{3}$. И $ F_{\eta}(x)=F_{\xi}(\frac{x-18}{3}) $.

Задача 3. Известно, что случайная величина $\xi$ имеет нормальное $N(0,1)$ распределение. Найдите функцию распределения и плотность случайной величины $\eta={\xi}^4$.

Решение:

Я думаю, здесь тоже следует предположить, что $ f_{\xi}(x) $ И $ F_{\xi} (x) $ Известные функции Но $g(x)=x^4$ немонотонная функция, и я получил нечто абсурдное.

$F_{\eta}(x)= F_{\xi}(x^{1/4}) $ , когда $x \geq 0 $ и $F_{\eta}(x)=1- F_{\xi}(-x^{1/4})$ , когда $x<0$

$f_{\eta}(x)=(F_{\eta}(x))'_{x}=\frac{1}{4}f_{\xi}(x^{1/4})|x^{-3/4}|$

Не могу связать задания с теорией. Я сомневаюсь, что решение, ДАЖЕ первой задачи верное.

[Combat Zone]

У нее условие неверное )
$f_\xi$ - не плотность. Отнормируйте как следует.

А чтоб не сомневаться, где тут монотонность правильно приткнута, а где нет, я такие задания по готовой формуле никогда не решаю. Лучше всегда начинать с поисков функции того распределения, которое нужно найти. Прямо по определению. Тогда и немонотонные решатся спокойно.

[paranoidandroid]

То есть, здесь рассматриваем только интервал (0,1)? Тогда функция $g(x)=x^4$ на этом интервале монотонна и все хорошо..