Арифметические прогрессии из простых чисел

[Dmitriy40]

Не нашёл обсуждения конкретно этого вопроса, создам новую тему.

Ранее были известны как минимум такие ограничения на PAP-22 (или AP-22) с минимальным диаметром (т.е. все 22 числа простые):

$$11410337850553 + 475180 \cdot 19\# \cdot n, n=0 \ldots 21$$

$$403185216600637 + 219029 \cdot 19\# \cdot n, n=0 \ldots 22$$

$$497003857949969 + 179998 \cdot 19\# \cdot n, n=0 \ldots 21$$

$$19261849254523 + 80910 \cdot 19\# \cdot n, n=0 \ldots 21$$

$$166537312120867 + 9959 \cdot 19\# \cdot n, n=0 \ldots 21$$

Взяты со страниц https://www.pzktupel.de/PAP/RHMINDIFF.php и https://www.pzktupel.de/PAP/RHMINEND.php (либо с длиннющей страницы с более старыми данными http://primerecords.dk/aprecords.htm ).

Теперь нашёл меньшее значение диаметра:

$$1294130773627333 + 2615 \cdot 19\# \cdot n, n=0 \ldots 21$$

Потребовалось всего 22ч счёта в 64 потока на 2ГГц (плюс месяцы на написание и доработки программы).

[Dmitriy40]

О, pzktupel.de уже обновили, писал им на email.

[Yadryara]

Поздравляю! Пока толком не вникал, понял только что это новый мировой рекорд.

[Dmitriy40]

В общем да, рекорд. Странно что так мало времени потребовалось его найти, меньше суток счёта, почему не нашли раньше. Правда ещё сутки на компиляцию 9959 программ и несколько дней на подбор разбиений (с промежуточными тестами).
А вникать тут некуда, просто паттерн диаметром 2615*21*19#: v=[0..21]*19#*2615. "Грязный" по нашей терминологии, с кучей лишних простых внутри кортежа. Как раз для этого и сделал диаметры больше и 256 и 2^32.

[Dmitriy40]

Новое улучшение минимального диаметра для PAP/AP-22:

$$46088665875716819+2141 \cdot 19\# \cdot n, n=0 \ldots 21$$

Потребовалось больше 10 дней счёта.

[mathpath]

Прогрессия длины 27 (мировой рекорд)

Найдена в 2024 году командой математиков (проект PrimeGrid).

Первое число: p=224584605939537911+81292139×23#×np=224584605939537911+81292139×23#×n (очень большое).

Разность: d=23#=223092870d=23#=223092870 (примориал 23).

Длина: 27 простых чисел подряд.

-- 22.05.2025, 13:17 --

Прогрессия длины 26

Найдена в 2023 году (также PrimeGrid).

Первое число: p=3486107472997423+371891575525470×np=3486107472997423+371891575525470×n.

-- 22.05.2025, 13:18 --

Прогрессия длины 25

Найдена в 2008 году (проект Benoît Perichon и Jarosław Wróblewski).

Первое число: p=6171054912832631+366384×23#×np=6171054912832631+366384×23#×n.

[Dmitriy40]

mathpath
И что хотели этим сказать? Я не искал самую длинную AP-k.
Прежде чем писать могли бы сходить по ссылкам и посмотреть о чём речь.

mathpath в сообщении #1687026 писал(а):

Длина: 27 простых чисел подряд.

А выделенное жирным - просто неверно, простые не подряд!

И кстати даты для AP26 и AP27 у Вас похоже неправильные: https://www.pzktupel.de/PAP/aprecords.php - тут в первой табличке указаны (для AP26 - существенно) более ранние.

[B@R5uk]

Что значит запись "19-решётка"?

-- 06.06.2025, 15:57 --

Впрочем, нашёл:

Цитата:

k# (called k primorial) is the product of all primes ≤ k, e.g. 10# = 2 • 3 • 5 • 7.
2# = 2, 3# = 6, 5# =30, 7# = 210, 11# = 2310, 13# = 30030, 17# = 510510, 19# = 9699690, 23# = 223092870.

[bondkim137]

(Оффтоп)

Dmitriy40, а я сначала подумал, вы путь к ключам криптокошелька какого-то несильно защищенного коина нащупали А оказалось, это спорт.
Поздравляю с рекордом!

[mathpath]

Дипсик говорит, что для первого миллиона простых чисел можно ожидать:
Множество прогрессий длины 3-10
Возможно, прогрессии длины 10-15
Маловероятно найти прогрессии длины > 20
Действительно, я довольно быстро нашел арифметическую последовательность длиной=13, начало=4943, разность=60060

[Dmitriy40]

Первый миллион не интересен, там давно всё интересное найдено, да и ищется оно за секунды-минуты даже если и придумать что-то новое. Сейчас интересное начинается после квадриллиона ($10^{15}$) или выше $10^{20}$.

[Dmitriy40]

mathpath в сообщении #1716270 писал(а):

Возможно, прогрессии длины 10-15
Маловероятно найти прогрессии длины > 20

ИИ конечно молодец, очевидности вытаскивает "на ура" - такие цепочки давно известны, например до 1.3e16 есть цепочки длиной до 26 чисел. А до 3.685e7 точно нет цепочек длиннее 13 чисел.

[gris]

Забавное: поискал по наущению нашего товарища арифметические прогрессии из простых, которые склеиваются в простое число: $[5, 17, 29, 41, 53] \to 517294153$. Жаль, что привязано к десятичной системе счисления На уровне пятиклассника доказал, что таковых длиной кратной трём не существует Мой рекорд
10939 9694459 19377979 29061499 38745019 48428539 58112059 67795579 77479099 87162619

[waxtep]

gris в сообщении #1718565 писал(а):

Мой рекорд
10939 9694459 19377979 29061499 38745019 48428539 58112059 67795579 77479099 87162619

Мощно. Я, честно говоря, не ожидал, что PARI проверит простоту такого монстра в мгновение ока.

gris в сообщении #1718565 писал(а):

Жаль, что привязано к десятичной системе счисления

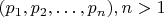
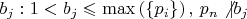
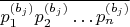
Можно попробовать такое обобщение-извращение: пусть дана последовательность (необязательно всех различающихся) простых $(p_1,p_2,\ldots,p_n), n>1$. И для нее последовательность оснований позиционной системы счисления $b_j: 1<b_j\leqslant \max\left(\{p_i\}\right),\, p_n \not | b_j$ и записей чисел $\overline{p_1^{(b_j)}p_2^{(b_j)}\ldots p_n^{(b_j)}}$. Будем искать последовательности, где все записанные таким образом числа - простые. 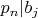Для $p_n | b_j$ можно дополнительно потребовать простоты $\overline{p_1^{(b_j)}p_2^{(b_j)}\ldots p_n^{(b_j)}}/p_n$.

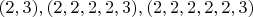
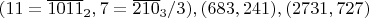
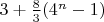
В таком аспекте, конечно, приятнее всего работать с двойками и тройками (это уже частный пример), вот, последовательности $(2,3), (2,2,2,2,3), (2,2,2,2,2,3)$ удовлетворяют и основному условию и дополнительному: все числа в парах $(11=\overline{1011}_2,7=\overline{210}_3/3),(683,241),(2731,727)$ - простые. В этом примере речь идет об одновременной простоте чисел вида $3+\frac83(4^n-1)$ и $3^{n+1}-2$. 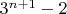Конечно ли их число? Если да, можно поискать наибольшее. Или, побаловаться с общим случаем как-то еще. Долой десятичное рабство!

-- 21.02.2026, 12:51 --

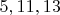
Эти трое, кстати, и в "единичной" системе просты - $5,11,13$. Можно добавить сверх-дополнительное требование простоты $2n+3$

-- 21.02.2026, 13:21 --

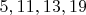
Хм, это интересно: до $10000$ только четыре простых числа $5,11,13,19$ таковы, что одновременно просты и $\frac13(2^p+1), \, 3^{\frac{p-1}2}-2$

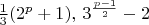-- 21.02.2026, 13:29 --

Вообще это конечно здесь не очень в тему, посвященную прогрессиям, пардон

[waxtep]

waxtep в сообщении #1718678 писал(а):

Хм, это интересно: до $10000$ только четыре простых числа $5,11,13,19$ таковы, что одновременно просты и $\frac13(2^p+1), \, 3^{\frac{p-1}2}-2$

Вообще это конечно здесь не очень в тему, посвященную прогрессиям, пардон

Все же, чтобы замкнуть это ответвление; простые вида $3^k-2$ судя по всему привлекли немного внимания математической общественности: A014232. А простые вида $\frac13(2^p+1)$ очень даже да:
A000978
Простое число Вагстафа
https://mathworld.wolfram.com/WagstaffPrime.html
https://mathworld.wolfram.com/NewMersennePrimeConjecture.html