Доказал, что для любого приведённого многочлена степени

можно выполнить разделение на вещественную и мнимую часть через определители, скидываю сюда короткое доказательство.
Матричное представление многочленов с комплексными корнями и разложение на вещественную/мнимую частиВведениеРассмотрим приведённый многочлен степени

с комплексными корнями:

Положим

,

. Цель работы — доказать:
1. Представление

как определителя

-матрицы
2. Разложение определителя на компоненты

и

3. Зависимость характера компонент от чётности
 Обоснование размера
Обоснование размера 
Для произвольных

матрица

с вещественными элементами, линейными по

,
не подходит. Контрпример при

:
Пусть

. Предположим, существует матрица:

Тогда

имеет вещественные коэффициенты, но

— нет (коэффициент

).
Теорема о минимальной размерностиМинимальный размер матрицы для представления произвольного

—

. Обоснование:
1. Требуется выполнить условия:
-

-

- Старший коэффициент = 1
2. При

в матрице

возникает нулевой столбец
3. Структурно необходимо

условий для корней + 1 для старшего коэффициента
Конструкция матрицыОпределим матрицу

размера

:

где:
-

(диагональ)
-

(внедиагональные)
-

(последняя строка)
Теорема 1 (Основная) ДоказательствоЭтап 1: Корни многочлена
ДоказательствоЭтап 1: Корни многочленаПри

:
-

-

-

-й столбец нулевой
 Этап 2: Степень и старший коэффициент
Этап 2: Степень и старший коэффициентЭлементы линейны по

,


— многочлен степени

. Старшие члены:
- По

:

- По

: коэффициент

(из последней строки)
Совпадает с
 Этап 3: Тождество многочленов
Этап 3: Тождество многочленов
и

:
- Имеют одинаковые корни

- Одинаковые степени (

)
- Совпадают старшие коэффициенты
Следовательно, тождественно равны.
Теорема 2 (Разложение)
где

,

получены заменой последней строки:
-

:
![[B_1 \cdots B_n \ 0] [B_1 \cdots B_n \ 0]](https://dxdy-02.korotkov.co.uk/f/9/c/7/9c7223257ea6ec4f676410f63179139282.png)
-

:
![[0 \cdots 0 \ 1] [0 \cdots 0 \ 1]](https://dxdy-03.korotkov.co.uk/f/a/1/1/a1167d7febb6332dd9ab1a635a4c39da82.png)
При этом:
1.
 нечётно
нечётно:

,

2.
 чётно
чётно:
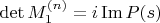
,
 ДоказательствоЛинейность определителя
ДоказательствоЛинейность определителя:

где
![U = [B_1 \cdots B_n \ 0] U = [B_1 \cdots B_n \ 0]](https://dxdy-03.korotkov.co.uk/f/2/3/6/2367e495ff7f6b8be0d8c2313e7dce7382.png)
,
![V = [0 \cdots 0 \ 1] V = [0 \cdots 0 \ 1]](https://dxdy-04.korotkov.co.uk/f/7/5/6/7561e62830bfba1fd68e5f367e6e972982.png)
.
Характер компонент:
-

-
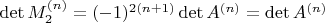
где

— подматрица первых

строк и столбцов.
Свойства миноров:
- В

(размер

):

Диагональные элементы:
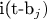

Число множителей

:

- В

: число множителей

:
 Анализ чётности
Анализ чётности:
1.
 нечётно
нечётно:
-

чётно

веществен
-

вещественны

веществен
-

нечётно

- Итог:

2.
 чётно
чётно:
-

нечётно

мним
-

чётно

веществен
- Итог:
 Пример для
Пример для 
Исходная матрица:

Разложение:

Так как

нечётно:
-

-
 Заключение
Заключение 1. Установлено минимальное представление

для произвольных комплексных корней
2. Получено разложение определителя на вещественную/мнимую части
3. Результаты могут быть применимы в:
- Численных методах (вычисления в

)
- Анализе устойчивости
- Построение линий уровня