Пусть

-- область, и задан линейный оператор
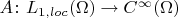
. Предположим, что оператор

обладает следующим свойством непрерывности: для любой функции
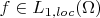
и любой последовательности функций

такой, что

для любой области с компактным замыканием

, выполнено

для любой функции

(т.е. с компактным носителем

).
Доказать, что тогда на самом деле функции

сходятся к

вместе со всеми своими частными производными равномерно на компактных подмножествах

(то есть

в пространстве Фреше

).