
Выделенное утверждение же не верно?
Рассмотрим на

неограниченный линейный функционал

. Пусть

,

, где

. Тогда

всюду плотно,

. При этом оператор проектирования
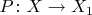
,

, являющийся оператором проектирования на

вдоль

, неограничен. Оператор проектирования

тогда тоже неограничен, т.к.

.
-- Пт апр 18, 2025 14:22:28 --Вот если бы одно подпространство было конечномерно, а другое замкнуто, то утверждение было бы верным: в любом нормированном пространстве алгебраическая прямая сумма замкнутого и конечномерного подпространств является топологической прямой суммой.