Помогите в градиентные методы оптимизации

[B@R5uk]

Пытаюсь тут по-глубже вникнуть в метод градиентного спуска и его обобщения, плавно переходя к более быстрым методам (порядка сходимости больше единицы) со второй производной. Раньше всегда пользовался Нелдером-Мидом (он очень устойчив к "плохим" целевым функциям, не требует производных и довольно быстро сходится), но сейчас в задаче производные считаются чуть ли не легче чем сама функция. Ну и размерность выше тоже. В связи с этим у меня возникли вопросы.

1. При выборе шага вдоль направления градиента можно использовать две стратегии: выбор новой точки с минимальным значением функции в ней или с минимальным значением нового градиента. Я правильно понимаю, что обе эти стратегии не являются наилучшими в плане быстродействия в общем случае? То есть для каждой из них есть "неудачные" ситуации.

2. Как скорость сходимости связана с размерностью задачи? Что-то нигде не нашёл упоминания. Может в какой-нибудь литературе есть конкретные формулы?

[dsge]

B@R5uk в сообщении #1682282 писал(а):

1. При выборе шага вдоль направления градиента можно использовать две стратегии: выбор новой точки с минимальным значением функции в ней или с минимальным значением нового градиента.

1-я стратегия может привести к тому, что большую часть времени вы будете решать одномерные задачи далеко от оптимума.

Широко используемый подход - это метод Armijo-Goldstein или backtracking. В направлении градиента необязательно находить минимум, главное чтобы целевая функция уменьшилась.

[мат-ламер]

B@R5uk в сообщении #1682282 писал(а):

В связи с этим у меня возникли вопросы.

Про какой конкретно метод у вас вопросы?

B@R5uk в сообщении #1682282 писал(а):

Пытаюсь тут по-глубже вникнуть в метод градиентного спуска и его обобщения, плавно переходя к более быстрым методам (

Про градиентный метод или про более быстрые?

B@R5uk в сообщении #1682282 писал(а):

или с минимальным значением нового градиента.

Градиент - вектор. В каком смысле - минимальное значение? Я что-то про такую стратегию не слышал.

B@R5uk в сообщении #1682282 писал(а):

Я правильно понимаю, что обе эти стратегии не являются наилучшими в плане быстродействия в общем случае? То есть для каждой из них есть "неудачные" ситуации.

Для градиентного метода все стратегии примерно одинаковые.

B@R5uk в сообщении #1682282 писал(а):

2. Как скорость сходимости связана с размерностью задачи?

Для градиентного метода вроде скорость сходимости от размера задачи не зависит. Она зависит от числа обусловленности матрицы Гесса.

B@R5uk в сообщении #1682282 писал(а):

Раньше всегда пользовался Нелдером-Мидом

У этого метода скорость сходимости падает с увеличением размерности.

B@R5uk в сообщении #1682282 писал(а):

плавно переходя к более быстрым методам (порядка сходимости больше единицы) со второй производной.

Тут вопрос более тонкий. Вы там используете метод с ограниченной памятью. Так скорость сходимости будет зависеть, насколько сильно вы эту память там ограничите. Другое дело, что для тех размерностей, что вы используете, степень ограничения памяти не существенена.

[zgemm]

B@R5uk в сообщении #1682282 писал(а):

Пытаюсь тут по-глубже вникнуть в метод градиентного спуска и его обобщения, плавно переходя к более быстрым методам (порядка сходимости больше единицы) со второй производной.

я за свою жизнь писал много солверов именно для gradient-like методов минимизации, поэтому позвольте вставить свои семь копеек одной монетой.

Во-первых, надо понимать тип задачи и что у Вас твориться с градиентом. Если градиента нет, то надо подумать сможете ли Вы применить Баур-Штрассена, чтобы был градиент. Если не получается, на мой взгляд, от размерности 100 и выше надо окончательно отказаться от любых градиентных методов и что-то типа Недлера-Мида - самое оно. Для меньших размерностей - ну можно конечной разностью (центральной), но тоже, надо иметь возможность играться шагом, особенно если у Вас сильно не сбалансированные направления.

Если градиент есть, почти всегда катит LM-BFGS, если есть очень плохие овраги, или хотя бы пара минимумов, надо поверх прикручивать рестарты, причем эти рестарты должны плавно переходить в отжиг, если овражность очень плохая и минимумов много.

Одномерную минимизацию тоже надо городить, причем очень вдумчиво. Обычно ее под каждую задачу надо настраивать, то есть где-то, где стоимость вычисления функции большая, надо делать поменьше одномерных шагов, а где-то наоборот.

Также надо помнить, что BFGSы - не панацея, у Вас в солвере всегда долна быть возможность переключиться на сопряженный градиент, на обычных градиент и Вам надо это делать если BFGSное направление стало не успешным. У меня там 7 вариантов, в том числе и Недлер, причем выбор - очень с элементами ИИ - по-другому - никак.

Все это приводит к эдакому искусству. Я свое искусство отлаживал на задаче, в которой есть хроматографическая колонка, в этой колонке сотня тарелок, на каждой тарелке устанавливается равновесие (с десяток параметров) и это надо повторять во времени тысячи и десятки тысяч раз. Один раз не сойдется - все на выброс. Потом у меня появились аналогичные задачи с сотней неизвестных и таким же числом раз на минимизацию, все пошло юзом, но после прикручивания множества вспомогательных параметров все снова заработало. Потом черт меня дернул считать довольно простую задачу минимизации с миллиардом неизвестных. Тут вылезло еще с десяток новых параметров, но, все-таки заработало.

То есть я к тому, что хоть я в своей жизни много раз этим занимался, я не считаю, что владею самым лучшим солвером в мире, но все доступные готовые библиотечные солверы, моему солверу на моих задачах проигрывают.

Про дискретную минимизацию сказать ничего не могу, отжигом много раз что-то решал, но совершенно не считаю себя в дискретной минимизации хоть на сколько-то экспертом.

[zgemm]

мат-ламер в сообщении #1682294 писал(а):

Тут вопрос более тонкий. Вы там используете метод с ограниченной памятью. Так скорость сходимости будет зависеть, насколько сильно вы эту память там ограничите. Другое дело, что для тех размерностей, что вы используете, степень ограничения памяти не существенена.

позвольте, пожалуйста, и тут вставить свои семь копеек...

Я по началу тоже думал, что основной смысл LM-BFGS - это работа с огромными размерностями и ограничение расхода памяти. Начал я как-то экспериментировать и этим методом для тех размерностей, где можно делать что угодно. Так вот ограничение этого подпространства часто просто полезно, так как сходится быстрее. Где-то я даже видел к этому обоснование, но аргументированно его пересказать не смогу.

[B@R5uk]

мат-ламер в сообщении #1682294 писал(а):

Про градиентный метод или про более быстрые?

zgemm в сообщении #1682295 писал(а):

Во-первых, надо понимать тип задачи и что у Вас твориться с градиентом.

Пока обсасываю основы, то есть обычный градиентный метод и модельная задача

$$f(x):\mathbb{R}^N\to\mathbb{R},\qquad\qquad f(x)=x^TAx,\qquad\qquad A^T=A$$

Хочу понять, что влияет на сходимость различных стратегий выбора шага, какие случаи плохие, как их детектировать и что делать при обнаружении "ситуации". Когда это в голове устаканится перейду к суперэкспоненциальным методам. Тем более, что они, как правило, требуют от целевой функции больше хороших свойств, из-за чего применимы только в достаточной близости к экстремуму, а вне этой области придётся пользоваться чем-то по-проще. Чтобы не прогадать с моментом перехода от одного к другому надо знать, как ведут себя оба метода, в том числе простой.

мат-ламер в сообщении #1682294 писал(а):

Для градиентного метода вроде скорость сходимости от размера задачи не зависит. Она зависит от числа обусловленности матрицы Гесса.

Спасибо! Накатал по-быстрому программку примитивную потестить: никакой разницы, что 4 измерения, что 400. Правда, я пока только с фиксированным шагом тестил.

мат-ламер в сообщении #1682294 писал(а):

Для градиентного метода все стратегии примерно одинаковые.

Опять же, я тут в программке сейчас немного поигрался с фиксированным шагом, его выбор зависит от целевой функции, и есть некоторое оптимальное значение, дающее наибольшую скорость. Интересно, как это рассчитать?

мат-ламер в сообщении #1682294 писал(а):

У этого метода скорость сходимости падает с увеличением размерности.

Спасибо! Я из практики подозревал, но не знал как факт. Хотелось бы ещё и конкретное число, конечно.

мат-ламер в сообщении #1682294 писал(а):

Градиент - вектор. В каком смысле - минимальное значение? Я что-то про такую стратегию не слышал.

Ну дык! По модулю разумеется. Как мы определяем, что находимся в минимуме? Целевая функция минимальна, и её градиент равен нулю. Отсюда сразу следуют две жадные стратегии: на каждом шаге выбирать такой, чтобы либо функция, либо модуль её градиента были минимальны в новой точке. Хочется же как можно быстрее придти в минимум.

мат-ламер в сообщении #1682294 писал(а):

Тут вопрос более тонкий. Вы там используете метод с ограниченной памятью. Так скорость сходимости будет зависеть, насколько сильно вы эту память там ограничите.

Я так понимаю вы говорите про L-BFGS? Если да, то спасибо за информацию. Я даже не вникал что к чему с ним, немного глянул про BFGS, узнал, что он аппроксимирует матрицу, обратную матрице Гёссе, что значит он является квазиньютоновским и должен сходится быстрее градиентного, но пока не нашёл, чему она равна (ни степень, ни скорость). Матрица кажется накладным делом, если много неизвестных. Если же матрица Гёссе целевой функции легко считается и сильно разрежена, то стоит задуматься о том, чтобы считать умножение на её обратную методом сопряжённого градиента с небольшой точностью, что потребует создания отдельного метода. Но это пока только мечты и общие соображения.

(Оффтоп)

Программка:

Используется синтаксис Matlab M

%   File: study_GD.m
%   dxdy.ru/topic160189.html
%   B@R5uk, 2025, April

clc
clearvars
format compact
%format long
format short

type_A = 2;
rand_x = 0;
num_dim = 4;
num_steps = 50;

func_objective = @(x, A) 0.5 * x' * A * x;
func_gradient  = @(x, A)            A * x;

switch type_A
    case 1
        A = eye (num_dim);
    case 2
        A = eye (num_dim);
        A (1) = 2;
    otherwise
        A = randn (num_dim);
        [v d] = eig (A + A');
        A = v * (abs (d) + eye (num_dim)) * v';
end
if rand_x
    x0 = randn (num_dim, 1);
    x0 = x0 / sqrt (sum (x0 .^2));
else
    x0 = zeros (num_dim, 1);
    x0 (1) = 0.000000001;
    x0 (2) = 1;
end
step = 0.9;

history_value = zeros (num_steps, 1);
history_argum = zeros (num_steps, num_dim);
history_grad  = zeros (num_steps, num_dim);

x = x0;
flag_run = 0;
k = 0;
while k < num_steps
    k = k + 1;
    p = func_gradient (x, A);
    x = x - step * p;
    history_value (k) = func_objective (x, A);
    history_argum (k, :) = x;
    history_grad  (k, :) = p;
end

rate = [ones(num_steps - 15, 1) (16 : num_steps)'] \ log10 (sqrt (sum (history_argum (16 : end, :) .^ 2, 2)));

subplot (3, 1, [1 2])
xx = -1 : 0.05 : 1;
zz = zeros (size (xx, 2));
for k = 1 : numel (xx)
    for l = 1 : numel (xx)
        zz (k, l) = func_objective ([xx(k); xx(l); zeros(num_dim - 2, 1)], A);
    end
end
contourf (xx, xx, zz, 0 : 0.1 : 3)
%colorbar
hold on
plot ([x0(1); history_argum(:, 1)], [x0(2); history_argum(:, 2)], 'w.-')
hold off
axis equal
title (['Dimentions: ', num2str(num_dim)])
xlim ([-1 1])
ylim ([-1 1])

subplot (313)
semilogy ([0 num_steps], 10 .^ (rate(1) + rate(2) * [0 num_steps]), 'k')
hold on
semilogy (0 : num_steps, sqrt (abs ([func_objective(x0, A); history_value])))
semilogy (0 : num_steps, sqrt (sum ([x0'; history_argum] .^ 2, 2)), 'r')
semilogy (0 : num_steps, sqrt (sum ([func_gradient(x0, A)'; history_grad] .^ 2, 2)), 'g')
hold off
grid on
xlim ([0 num_steps])
ylim ([1e-15 1])
if 0 > rate (2)
    title (['Descent rate ', num2str(-rate (2)), ' digits per step'])
else
    title (['Ascent rate ', num2str(rate (2)), ' digits per step'])
end
legend ('Line approximation', 'Objective rooted', 'Argument module', 'Gradient module')
xlabel ('Step number')
 

[zgemm]

B@R5uk в сообщении #1682339 писал(а):

Пока обсасываю основы, то есть обычный градиентный метод и модельная задача

$$f(x):\mathbb{R}^N\to\mathbb{R},\qquad\qquad f(x)=x^TAx,\qquad\qquad A^T=A$$

Хочу понять, что влияет на сходимость различных стратегий выбора шага, какие случаи плохие, как их детектировать и что делать при обнаружении "ситуации".

возьмите полилинейную хотя бы задачу, в случае с квадратичной, как вы предложили, все BFGSы будут себя вести как Ланцош или BiCGStab. Там совсем другая специфика!!!

Возьмите классику

$$E = x^T \operatorname{diag}(x) A \operatorname{diag} (x) x + (x^T B x)^2$$

с симметричными матрицами $A$ и $B$, или пусть даже это будет одна и та же матрица.

[B@R5uk]

zgemm, у этой целевой функции в минимуме ноль 4-го порядка вместо 2-го. Может быть у второго слагаемого квадрат не нужен? В любом случае, спасибо, возьму на заметку.

[zgemm]

B@R5uk в сообщении #1682353 писал(а):

zgemm, у этой целевой функции в минимуме ноль 4-го порядка вместо 2-го. Может быть у второго слагаемого квадрат не нужен? В любом случае, спасибо, возьму на заметку.

Без квадрата во втором члене у Вас снова будет Ланцош с поправками. А если первый член выбросить - будет тривиальное решение.

Во втором члене матрица может быть любой и не симметричной, а в первом должна быть хотя бы не отрицательно определённой.

На поиграться очень рекомендую брать обе матрицы вырожденные, эдак с рангом 2/3 от размерности. BFGS уже будут хорошо задыхаться по оврагам, и всегда можно вычислить честное ньютоновское направление и с ним сравниться.

[B@R5uk]

Хорошо, сообразил, что происходит в градиентном спуске при фиксированном шаге, почему он начинает прыгать при больших значениях шага и когда сходится.

Пусть матрица A задачи является симметричной и положительно определённой.

$$y=\frac{1}{2}x^TAx,\qquad\qquad A^T=A$$

Направление, противоположное направлению градиента является направлением спуска c фиксированным шагом β:

$$p=-\frac{dy}{dx}=Ax$$

$$x_{k+1}=x_k+\beta p_k$$

Эта простая квадратичная задача очень хороша здесь в плане удобности анализа, потому что шаг метода в этом случае является линейным преобразованием вектора аппроксимации решения:

$$x_{k+1}=x_k+\beta p_k=x_k-\beta Ax_k=\bigl(I-\beta A\bigr)x_k=S\bigl(\beta\bigr)x_k$$

$$x_k=S^k\bigl(\beta\bigr)x_0=\bigl(I-\beta A\bigr)^kx_0$$

Где S — оператор шага. Поскольку матрица A симметрична, она имеет спектральное разложение, а поскольку она положительно определена, все её собственные значения строго больше нуля. Пронумеруем индексом 1 элемент с наибольшим значением, а индексом 2 — с наименьшим.

$$A=Q\Lambda_0 Q^T,\qquad\qquad QQ^T=I$$

$$S^k\bigl(\beta\bigr)=\bigl(I-\beta A\bigr)^k=\bigl(QQ^T-\beta Q\Lambda_0 Q^T\bigr)^k=Q\bigl(I-\beta\Lambda_0\bigr)^kQ^T=Q\Lambda^k\bigl(\beta\bigr)Q^T$$

$$\Lambda_0=\left(\begin{matrix}\lambda_1&0&\ldots\\0&\lambda_2&\\\vdots&&\ddots\end{matrix}\right),\qquad\qquad\Lambda\bigl(\beta\bigr)=I-\beta\Lambda_0=\left(\begin{matrix}1-\beta\lambda_1&0&\ldots\\0&1-\beta\lambda_2&\\\vdots&&\ddots\end{matrix}\right)$$

То есть, переход от начального приближения к приближению на k-ом шаге заключается в масштабировании системы координат вдоль направлений собственных векторов оператора шага S (которые совпадают с направлениями оператора A) на величины, равные k-ой степени соответствующих собственных чисел оператора S, выражаемых через собственные числа оператора A. Это означает, что можно сразу перейти в систему координат, заданную собственными векторами оператора A, и рассматривать только диагональные матрицы.

В этой задаче можно даже точно определить, когда метод сходится. Для этого нужно, чтобы все собственные значения оператора шага S были по модулю меньше единицы, тогда их степени будут стремиться к нулю экспоненциально (сходимость первого порядка). С помощью положительного коэффициента β эти значения линейно выражаются через значения оператора A, которые все тоже положительны и заключены на отрезке, концы которого заданы его максимальным и минимальным собственными значениями:

$$0<\lambda_2\le\lambda_m\le\lambda_1,\qquad\qquad 3\le m\le N$$

$$\bigl|1-\beta\lambda_n\bigr|<1,\qquad\qquad 1\le n\le N$$

$$-1<1-\beta\lambda_n<1$$

$$-2<-\beta\lambda_n<0$$

$$0<\beta\lambda_n<2$$

$$\beta<\frac{2}{\lambda_n}$$

Левое неравенство в предпоследней строчке выполнено автоматически, потому что мы рассматриваем положительные величины, а второе будет выполнено для всех n, если параметр шага β меньше некоторого критического значения, определяемого только наибольшим собственным значением оператора A:

$$\beta<\beta_\text{crit}=\frac{2}{\lambda_1}$$

Надо заметить, что если положить шаг равным критическому, то одно из собственных значений оператора шага S будет равно -1, а все остальные будут по модулю меньше 1. Поэтому траектория "спуска" будет стремится к траектории, прыгающей между двумя точками, направления на которые от минимума будут задаваться собственным вектором оператора A, соответствующим максимальному собственному значению этого оператора. Величина -1, возводимая в чётные и нечётные степени, другими словами. Это в том числе, объясняет почему вообще траектории бывают зигзагом: координаты разложения вектора приближения x по базису собственных векторов операторов A и S будут менять знак, если в операторе шага S имеются отрицательные собственные значения. Однако, это объяснение верно только для градиентного спуска с фиксированным шагом, при других стратегиях выбора шага причины будут другими.

Можно даже найти параметр шага, соответствующий наискорейшему спуску. Для этого требуется, чтобы все собственные значения оператора шага S были как можно меньше, потолок при этом определит скорость спуска. Поскольку все собственные значения оператора A заключены на отрезке с положительными концами, необходимо лишь удовлетворить это требование для концов отрезка, для промежуточных значений это будет выполнено автоматически. Другими словами, для градиентного спуска размерность задачи не влияет на сходимость.

$$\bigl|1-\beta_\text{best}\lambda_1\bigr|=\bigl|1-\beta_\text{best}\lambda_2\bigr|=r$$

При этом под правым модулем окажется положительная величина (поскольку вычитаемая мала), а под левым — отрицательная. По этой причине факт того, что траектория представляет зигзаг, является признаком как близости величины шага к оптимальному, так и к критическому (с оговоркой на фиксированность шага).

$$-1+\beta_\text{best}\lambda_1=1-\beta_\text{best}\lambda_2=r$$

Откуда оптимальная величина шага

$$\beta_\text{best}=\frac{2}{\lambda_1+\lambda_2},\qquad\qquad r=\frac{\lambda_1-\lambda_2}{\lambda_1+\lambda_2}$$

И скорость сходимости в десятичных знаках на шаг будет равна

$$\rho=-\log_{10}(r)=-\log_{10}\left(\frac{\lambda_1-\lambda_2}{\lambda_1+\lambda_2}\right)$$

В случае, когда собственные значения оператора A значительно отличаются по порядку, то величина r будет близка к единице и скорость сходимости в десятичных знаках на шаг окажется

$$\rho=-\frac{1}{\ln 10}\ln\left(1-\frac{2\lambda_2}{\lambda_1+\lambda_2}\right)\approx\frac{2}{\ln 10}\cdot\frac{\lambda_2}{\lambda_1}$$

То есть, очень малой. Интересно, какие вообще методы борьбы с этим существуют?

Если же известно, что задача более-менее хорошо обусловлена — собственные значения оператора A квадратичной формы вблизи минимума приблизительно одного порядка, — но они неизвестны, то сразу напрашивается следующая стратегия "подкручивания" величины фиксированного шага. Выбираем из каких-то эвристических или эмпирических соображений величину не сильно большую, но и не сильно маленькую. Начинаем градиентный спуск. Каждый раз, когда шаг алгоритма приводит к ухудшению целевой функции отбрасываем результат, умножаем величину шага, на константу меньшую единицы, и пробуем снова. Таким образом придём к величине шага, которая гарантированно меньше критической, но не обязательно близка к оптимальной. Чтобы "нащупать" оптимальную величину, потребуются дополнительные усилия, которые должны в том числе учитывать, что аппроксимация решения на данном шаге может быть вдали от минимума, что означает, целевая функция не будет иметь рассматриваемый выше вид N+1-мерного эллиптического параболоида. Стоит ещё заметить, что критическая и оптимальная величины шага для случая, когда все собственные числа равны отличаются в 2 раза. Возможно, это тоже можно использовать. Например, если каким-то образом заметить, что зигзаг в траектории решения отсутствует, то можно увеличить величину шага почти в 2 раза.

В случае, если просто заранее задались величиной неизменного шага, то скорость сходимости будет:

$$r=\max\limits_{1\le n\le N}\bigl|1-\beta\lambda_n\bigr|$$

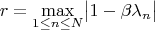
Степень сходимости при этом равна 1 (геометрическая прогрессия).

По идее, эта вся инфа должна быть в википедии в первых же абзацах, чтобы сразу врубиться в суть дела и не выводить всё это самостоятельно.

[мат-ламер]

B@R5uk в сообщении #1682495 писал(а):

Хорошо, сообразил, что происходит в градиентном спуске при фиксированном шаге

Тут ещё что понимать под фиксированным шагом. Можно понимать буквально. На начальных этапах оптимизации это может прокатить. Но вблизи экстремума метод будет прыгать туда-сюда. Но можно понимать, что мы умножаем некий фиксированный множитель на антиградиент (если ищем минимум). Это работает. Но тут вопрос - а как выбрать этот множитель? Если нет никакой информации насчёт функции, то таки надо делать хотя бы неполную оптимизацию вдоль выбранного направления.

[мат-ламер]

B@R5uk в сообщении #1682495 писал(а):

Это в том числе, объясняет почему вообще траектории бывают зигзагом

Для метода наискорейшего спуска это очевидно. В нём оптимизация вдоль заданного направления идёт до тех пор, пока производная вдоль этого направления не занулится. Градиент в этой точке будет перпендикулярен нашему заданному направлению.

[zgemm]

B@R5uk в сообщении #1682495 писал(а):

В случае, когда собственные значения оператора A значительно отличаются по порядку, то величина r будет близка к единице и скорость сходимости в десятичных знаках на шаг окажется

$$\rho=-\frac{1}{\ln 10}\ln\left(1-\frac{2\lambda_2}{\lambda_1+\lambda_2}\right)\approx\frac{2}{\ln 10}\cdot\frac{\lambda_2}{\lambda_1}$$

То есть, очень малой. Интересно, какие вообще методы борьбы с этим существуют?

Я Вам уже перечислял - это тот же самый сопряженный градиент хотя бы.

Не знаю, почему в википедии этого еще нет (мне прямо сейчас немного лениво учебники в википедию переписывать), но можно найти книжки Деммеля или почитать в кратком курсе численного анализа у Тыртышникова - книжки кстати 90-х годов. Вообще-то это классика, мне эту классику на 3-ем курсе в 90-х уже преподавали.

Но опять же, повторю свое замечание выше по поводу того, что квадратичные и все остальные задачи - существенно отличаются, причем теория и практика существенно отличаются.

[B@R5uk]

zgemm в сообщении #1682527 писал(а):

что квадратичные и все остальные задачи - существенно отличаются, причем теория и практика существенно отличаются.

Ну понятное дело, что когда функция в дали от минимума, то она может вести себя как угодно. Там и седловые точки всяких разных порядков (не в смысле "седловая точка", где все производные равны нулю, а вторые образуют "знаконеопределённую" форму, а в смысле, что поверхность в окрестности лежит по обе стороны от касательной плоскости (к N+1-мерному графику)) и даже просто смена направления выпуклости. Однако, вблизи минимума (хорошего, гладкого, а не как в некоторых задачах) любая функция будет вести себя квадратично. По этой причине, на мой взгляд, очень логично изучить то, как всевозможные методы (в том числе самые простые) ведут себя на таких функциях. Ясное дело, что малые поправки третьей и более высоких степеней, которые отбрасываются из ряда Тейлора при анализе квадратичного приближения, будут вносить всякие гадости, но величина этих гадостей будет более высокого порядка малости по сравнению со свойствами изучаемых явлений. Особенно, когда дожимаешь последние 5-10 значащих цифр 16-значного числа (хотя, конечно, всякое бывает). Так что, когда они (свойства, в смысле) устойчивы к малым возмущениям, то весьма вероятно, что они сохранятся и в практическом случае.

За книжки спасибо, качну, гляну. До сопряжённого градиента пока не добрался по-вникать (вики клик-бэйтом не затянула), но тоже спасибо за напоминание.

[zgemm]

B@R5uk в сообщении #1682535 писал(а):

Особенно, когда дожимаешь последние 5-10 значащих цифр 16-значного числа (хотя, конечно, всякое бывает). Так что, когда они (свойства, в смысле) устойчивы к малым возмущениям, то весьма вероятно, что они сохранятся и в практическом случае.

не, я не это имел ввиду. Вы хотели изучать Ньютоновские и квази-Ньютоновские методы, так?

Для квадратичного функционала Гессиан всегда постоянен не зависимо где вы находитесь - у минимума, или очень далеко от него.

То есть Ньютон сойдется за один шаг, и это - постулат.

Квазиньютон - тоже будет хорошо сходиться, как только он саппроксимирует в себе Ньютоновскую матрицу.

А теперь задумайтесь что происходит для не квадратичных функционалов. Там Ньютон не может а-приори сойтись за один шаг, более того, он иногда ведет себя хуже, чем какой-нибудь градиентный метод с хорошей одномерной минимизацией. А вот квази-Ньютоны, особенно LM-BFGS как раз преследуют цель "угадать" как надо Гессиан поменять, когда мы уже далеко убежали по пространству. Если изучать именно это свойство (а Вы вроде бы настраивались на LM-BFGS), то Ваши квадратичные примеры вам только мешать будут, если просто что-то поминимизировать - да, с квадратичного функционала стоит начать.