Ещё попытка в эмпирический алгоритм. Набрасываем точки случайно. Затем вычисляем расстояния между точками. Находим минимальное расстояние. Затем для каждой из двух точек, расстояние между которыми минимально, находим три ближайшие и строим окружности через них. Точку, для которой радиус окружности больше, перемещаем в центр окружности. Пересчитываем расстояния. И т.д. Условие остановки непонятно, возможно, будет зацикливание.
находим три ближайшие и строим окружности через них.
Не взлетит. Три ближайшие точки могут оказаться почти на одной (сферической) прямой, что закинет передвигаемую точку непонятно куда, но точно не туда, куда хотелось бы. (Если я правильно понял алгоритм)...
В процессе штудирования "Численной оптимизации" Носедаля допёр до неожиданно простого и красивого способа определения того, является ли точка (назовём её
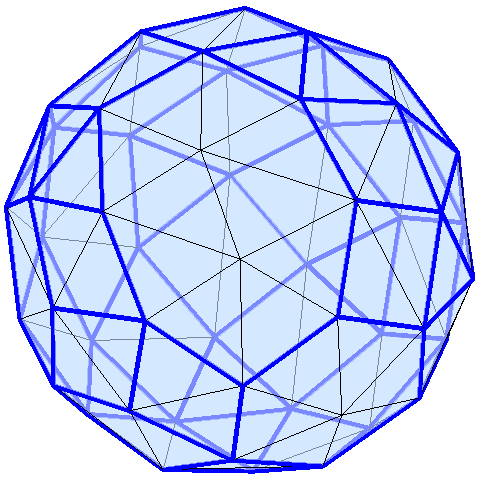
C — центр окружности) "зажатой" тремя равными по длине отрезками, выходящих из неё и заканчивающихся в трёх других точках. Демонстрационная картинка под катом:
(КАРТИНКА)
Ключевая идея заключается в том, чтобы рассмотреть задачу нахождения координат центра окружности:
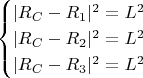
как оптимизационную задачу:
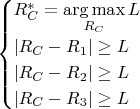
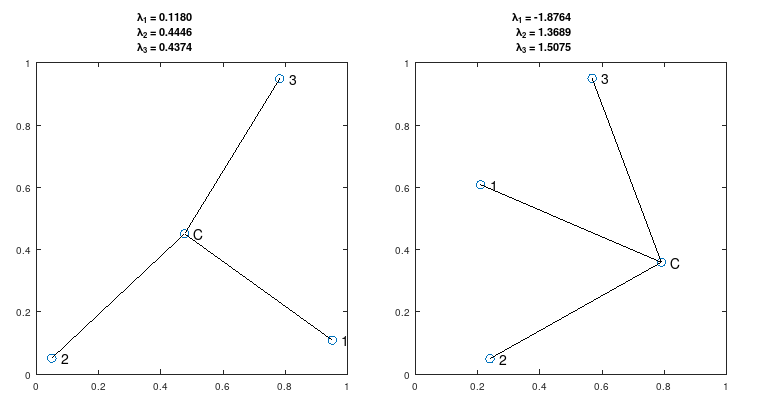
Решение у этих двух задач одно и то же (когда второе решение ограничено), но в процессе решения второй задачи мы получим множители Лагранжа, которые будут нести дополнительную (и представляющую непосредственный интерес) информацию. А именно: если знаки множителей одинаковы, то центр окружности "распирается" отрезками, соединяющими его с остальными тремя точками и расстояние до них нельзя монотонно увеличить непрерывным движением. Если же центр окружности лежит "в стороне" от трёх других точек, то один из множителей Лагранжа окажется отличного от двух других знака. В этом случае расстояние от
C до точек 1, 2 и 3 можно монотонно увеличивать. При этом ребро, соответствующее множителю Лагранжа с неправильным знаком можно выкинуть, потому что его длина всегда (в процессе увеличения длин рёбер) будет больше, чем двух других.
Формула для расчёта множителей Лагранжа получается такая (для квадратичных связей, без корня, в коде ниже сделано с корнем, различие только в численных значениях). Координаты центра окружности (со звездочками) берём из первой задачи (особенно для неограниченного случая), а множители рассчитываем по формуле для второй:
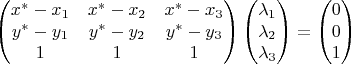
В случае сферической задачи всё будет то же самое, только добавится одна координата, одно ограничение равенством (принадлежность искомой точки сфере) и один множитель Лагранжа, соответствующий этому ограничению. Знак этого множителя никакого смысла нести не будет, так как ограничение в виде равенства, а не неравенства. Так же знаки множителей будут зависеть от того, как именно составляется функция Лагранжа и записываются неравенства. В разных книжках встречается по-разному. Код программы для рисования картинок (или просто потыкать и полюбоваться):
clc
clear all
names_str = '123C';
coords = 2 * pi * rand (1, 3);
coords = [cos(coords) 0; sin(coords) 0];
clim_min = min (coords, [], 2);
clim_max = max (coords, [], 2);
clim_diff = max (clim_max - clim_min);
coords = 0.5 * [1; 1] + 0.9 * (coords - repmat (0.5 * (clim_min + clim_max), 1, 4)) / clim_diff;
disp ([char(10) 'coords ='])
disp (coords)
mat_diff = zeros (3, 3);
for k = 1 : 3
coords_diff = coords (:, 4) - coords (:, k);
coords_diff = coords_diff / sqrt (sum (coords_diff .^ 2));
mat_diff (k, 1 : 2) = coords_diff;
end
mat_diff (:, end) = 1;
disp ([char(10) 'mat_diff ='])
disp (mat_diff)
mul_lagr = pinv (mat_diff') * [0 0 1]';
disp ([char(10) 'mul_lagr ='])
disp (mul_lagr)
clf reset
plot (coords (1, :), coords (2, :), 'o')
hold on
for k = 1 : 3
xx = coords (1, [k 4]);
yy = coords (2, [k 4]);
plot (xx, yy, 'k')
end
hold off
xlim ([0, 1])
ylim ([0, 1])
axis equal
for k = 1 : 4
text (0.03 + coords (1, k), coords (2, k), names_str (k), 'FontSize', 14)
end
title ({['\lambda_1 = ', num2str(mul_lagr (1), '% 6.4f')], ['\lambda_2 = ', num2str(mul_lagr (2), '% 6.4f')], ['\lambda_3 = ', num2str(mul_lagr (3), '% 6.4f')]}, 'HorizontalAlignment', 'Right')
set (gcf, 'GraphicsSmoothing', 'off')
А вообще, в общем случае поиска оптимального положения одной точки среди пачки других задачу можно решать через линейное программирование. Линеаризируем связи, оптимизируем смещение координат точки, применяем его к координатам, повторяем до победного. Сходимость (по моему опыту) будет (после "устаканивания" положения) квадратичной (удвоение числа значащих цифр решения за одну итерацию). Предложенный вами,
Евгений Машеров, алгоритм, сходится будет гарантированно, если на каждой итерации выбирать самое короткое ребро и из двух возможных вариантов движения выбирать тот, который даст наибольшее увеличение длины. Доказательство просто: рост длины кратчайшего ребра монотонен и ограничен сверху. Даже сходимость, скорее всего, будет линейная (отклонение от решения убывает по экспоненте). Однако, вот, фигура, к которой точки будут сходится, будет вызывать вопросы: скорее всего это будет набор точек в положении, при котором какое-то число рёбер имеют одинаковую длину, являющуюся минимальной. Алгоритм это гарантирует, а вот того, что число таких рёбер будет максимально (конфигурация локально оптимальна) алгоритм не гарантирует. Как дешёвую с точки зрения трудоёмкости начальную затравку можно использовать.
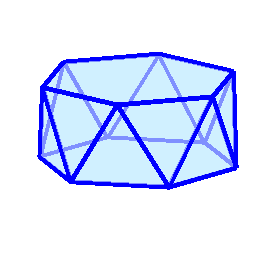
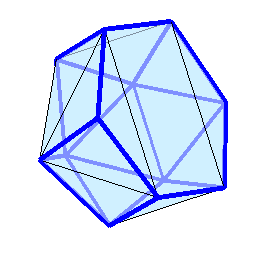
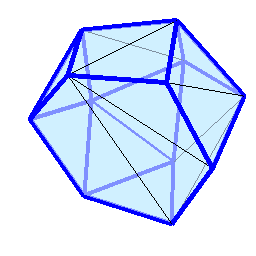
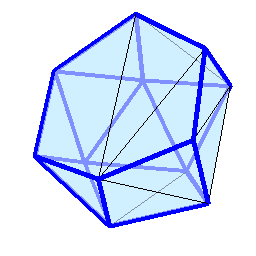
-- 13.12.2025, 19:23 --Потихоньку вырабатываю у себя такого рода интуитивное понимание на уровне "чуйки" в отношении того, как классическая оптимизация с ограничениями работает вообще и применительно к задаче Таммеса в частности. Кажется, что вот-вот уже хорошим годным солвером разрожусь, даже формула есть с квадратичной сходимостью, которая работает, когда все рёбра фигуры для оптимальной конфигурации корректно определены (не то, чтобы её было трудно составить, прочитав и поняв учебник Носедаля). И, вроде бы, понятно, как рёбра в рабочий набор потихоньку добавлять, однако, реализовать это всё дело в виде надёжно работающей закрытой процедуры всё никак не получается. Мерсссссские точки нулевой валентности ставят предо мной непреодолимую задачу: их присутствие снижает целевое число жёстких рёбер, к которому алгоритм должен стремиться в процессе оптимизации, в то же время, он не может начать эти точки искать, пока целевое число не достигнуто. Дожидаться достижения (с заданной точностью) предельного решения, прежде чем принимать решение о них с (возможным) последующим отбросом лишних ограничений — занятие неоптимальное даже с квадратичной сходимостью. Пока на этом деле у меня затык.

 . Это один из собственных векторов матрицы
. Это один из собственных векторов матрицы  , полученной произведением всех 6 элементарных трансвекций
, полученной произведением всех 6 элементарных трансвекций  при
при  в каком-то порядке.
в каком-то порядке. матрицы
матрицы  .
.
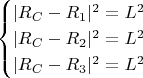 как оптимизационную задачу:
как оптимизационную задачу: 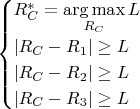 Решение у этих двух задач одно и то же (когда второе решение ограничено), но в процессе решения второй задачи мы получим множители Лагранжа, которые будут нести дополнительную (и представляющую непосредственный интерес) информацию. А именно: если знаки множителей одинаковы, то центр окружности "распирается" отрезками, соединяющими его с остальными тремя точками и расстояние до них нельзя монотонно увеличить непрерывным движением. Если же центр окружности лежит "в стороне" от трёх других точек, то один из множителей Лагранжа окажется отличного от двух других знака. В этом случае расстояние от
Решение у этих двух задач одно и то же (когда второе решение ограничено), но в процессе решения второй задачи мы получим множители Лагранжа, которые будут нести дополнительную (и представляющую непосредственный интерес) информацию. А именно: если знаки множителей одинаковы, то центр окружности "распирается" отрезками, соединяющими его с остальными тремя точками и расстояние до них нельзя монотонно увеличить непрерывным движением. Если же центр окружности лежит "в стороне" от трёх других точек, то один из множителей Лагранжа окажется отличного от двух других знака. В этом случае расстояние от 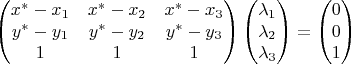 В случае сферической задачи всё будет то же самое, только добавится одна координата, одно ограничение равенством (принадлежность искомой точки сфере) и один множитель Лагранжа, соответствующий этому ограничению. Знак этого множителя никакого смысла нести не будет, так как ограничение в виде равенства, а не неравенства. Так же знаки множителей будут зависеть от того, как именно составляется функция Лагранжа и записываются неравенства. В разных книжках встречается по-разному. Код программы для рисования картинок (или просто потыкать и полюбоваться):
В случае сферической задачи всё будет то же самое, только добавится одна координата, одно ограничение равенством (принадлежность искомой точки сфере) и один множитель Лагранжа, соответствующий этому ограничению. Знак этого множителя никакого смысла нести не будет, так как ограничение в виде равенства, а не неравенства. Так же знаки множителей будут зависеть от того, как именно составляется функция Лагранжа и записываются неравенства. В разных книжках встречается по-разному. Код программы для рисования картинок (или просто потыкать и полюбоваться):