Строки и столбцы чисел Стирлинга независимо

[kthxbye]

Недавно по счастливой случайности обнаружил две пары рекурсивных тождеств для чисел Стирлинга, которые позволяют вычислять $n$-ую строку неависимо от всех остальных строк и $k$-ый столбец независимо от всех остальных столбцов.

Я предполагаю, что при $1 \leqslant k < n$ будем иметь

$$ {n \brack k} = \frac{1}{n-k} \sum\limits_{j=2}^{n-k+1} \binom{-k}{j}{n \brack k+j-1}(-1)^j, \\ {n \brack k} = \frac{1}{n-k} \sum\limits_{j=2}^{n-k+1} (j-2)!\binom{n}{j}{n-j+1 \brack k}. $$

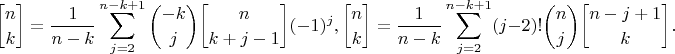
После взаимозамены $(-1)^j$ и $(j-2)!$, я также предполагаю, что при $1 \leqslant k < n$ будем иметь

$$ {n \brace k} = \frac{1}{n-k} \sum\limits_{j=2}^{n-k+1} (j-2)!\binom{-k}{j}{n \brace k+j-1}, \\ {n \brace k} = \frac{1}{n-k} \sum\limits_{j=2}^{n-k+1} \binom{n}{j}{n-j+1 \brace k}(-1)^j. $$

При некоторых $n$ и $k$ алгоритм, при котором мы заполняем числа Стирлинга в элементы массива (чтобы не вызывать их повторно для каждой новой суммы), домножая их на каждом следующем шаге на соотношение биномиальных коэффициентов (а также в двух из четырех случаев на соотношение факториалов), дает значительный выигрыш во времени по сравнению со стандартными формулами (сравнивал со встроенным в PARI/GP функциями).

Существует ли способ как-то доказать эти рекурсивные тождества?