Задача из Гохмана по терверу

[KurtMurt]

Привет всем! Прошу указать где я ошибаюсь - вроде все элементарно, а с ответом Гохмана не сходится

Случайная величина Х может иметь любое целое положительное значение n с вероятностью, пропорциональной $1/3^n$. Найти матожидание.
Фактически, задача сводится к нахождению суммы ряда $1/3 + 2/3^2 + 3/3^3 + ... n/3^n$
$M = 1/3 \cdot(1 + 2/3 + 3/3^2 + ... + n/3^{n-1})$
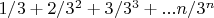
Сумму в скобках обозначаем S и находим по формуле для геометрической прогрессии:
$S - S/3 = 1 + 1/3 \cdot(2-1) + 1/3^2 \cdot(3-2) +... = 1 + 1/3 + 1/3^2 + ... = 1/(1 - 1/3) = 3/2$
Итого:
$ S(1 - 1/3)= 3/2 $
$S = 9/4$
$M(X) = S/3 = 3/4$
А у Гохмана в ответе 3/2. И в инете эта задача везде дублируется с этим же ответом. Значит ошибка у меня... но где???

[skobar]

Сумма всех вероятностей должна быть равна единице. Отсюда находим, что упомянутый коэффициент пропорциональности равен двойке, и ответ сходится.

[KurtMurt]

Спасибо! Не обратил внимание на использование слова "пропорциональной", а не "равной"...